


Empirical Testing of the CAPM and Relative Theories
Early tests of the CAPM were mildly supportive, but what works today looks nothing like those early approaches.
The CAPM was not solving a puzzle and did not integrate two previously disparate fields; it predicted something new: that returns were related to beta (the covariance of the asset and the market, divided by the variance of the market) and only beta, positively and linearly, through the formula
![]()
This is the Security Market Line, where the expected return rises linearly with the beta for any stock. It seemed like a straightforward theory.
Note there are expectation operators in front. As rm and ri are random variables, the best we can hope for is to see the
![]()
Note in equation (2.2), not only is there an error each period for each asset i, but betas and the risk free rate, can also change each period.
Treynor (1961), Sharpe (1964), Lintner (1965), and Mossin (1966), all derived the CAPM slightly differently. It is no coincidence that this coincided with the creation of the Center for Research in Security Prices (CRSP). At the behest of Merrill Lynch, two professors at the University of Chicago, James H. Lorie and Lawrence Fisher, created what has become the preeminent database on stocks in the United States. In 1964, their database was complete, and they successfully demonstrated the capabilities of computers by analyzing total return—dividends received as well as changes in capital as a result of price changes—of all common stocks listed on the NYSE from January 30, 1926, to through 1960.
The front page of the New York Times financial section heralded the pair’s their seminal article in the Journal of Business reported the average of the rates of return on common stocks listed on the NYSE was 9 percent. Now, this was which actually was within a couple percent of the return on the Dow Jones Industrial average, a simple price-weighted index of 30 prominent stocks. But, as this was within only 35 years of the Great Depression, it was rather shocking to learn that stocks, which were considered incredibly risky investments, had over a long period of time a seemingly dominant return premium over simply investing in bonds.
The result was extremely useful, both to stockbrokers, because it justified greater equity investment (and thus more commissions), and researchers, because it was consistent with the new risk-begets-return theory of the CAPM. For a researcher used to picking apart dog-eared books where many have treaded before, this truly was exciting. Rex Sinquefeld, now CEO of the quantitative equity management firm Dimensional Fund Advisors, noted, “If I had to rank events, I would say this one (the original CRSP Master File) is probably slightly more significant than the creation of the universe.” Virgin data, important data, imply one is like Kepler looking at Brache’s data on the positions of the planets—new laws are about to be discovered. The initial researchers would be Founding Fathers of this new field of scientific finance!
Sharpe (1966) published the first empirical test of the CAPM. He examined 34 mutual funds over 10 years, using annual returns. The nice thing about mutual funds, as opposed to stocks, is that presumably these funds are efficient, and have insignificant diversifiable risk. That is, risk which is unpriced, should not be held, so it probably is not. Sharpe tested the equation
![]()
Where a is the riskless return, and b presumably the price of risk. He found a=1.038, and b=0.836, consistent with the CAPM. Richard West (1968) noted that this test was almost meaningless. After all, if the test used the data from 1926 to 1935, b would have been negative if the CAPM held. It did not distinguish between idiosyncratic and systematic risk, or what kind of systematic risk. Recent tests on total volatility generally find negative b, highlighting Sharpe’s parochial result. Basically, he found a small sample, got the result expected, and a top journal gave it top billing because it seemed to confirm cutting edge theory.
Interestingly, the next empirical tests were not of the CAPM directly, but rather, applied the CAPM to the question of mutual fund performance persistence. The idea was that mutual fund managers often merely state their total return, and not a ‘risk-adjusted’ return. Treynor, Sharpe, and Jensen all looked at mutual fund performance using the CAPM to see if the mutual funds did demonstrate persistence, using
Sharpe (1967) looked at performance using the ‘reward-to-risk’ ratio:
![]()
Treynor and Mazuy (1966) used the following to detect market timing skill
![]()
Treynor (1965) used the following test
![]()
And Jensen (1969) introduced the term ‘alpha’ via his test using the CAPM
![]()
In general, they found that after fees, the mutual funds underperformed indices. Strangely, these early papers referencing this new theory were all applications, not tests. It’s as if without an alternative theory of risk and return, why test it?
George Douglas published the first remarkable empirical study of the CAPM in 1969. He applied a fairly straightforward test of the CAPM. He runs a regression on 500 stocks, each with five years of data, explaining the return based on their beta, and their residual variance.
![]()
With 500 different sets of betas, residual variances, and the average returns, he found that residual variance was significantly and positively correlated with returns—not beta. Lintner, one of the CAPM theoretical pioneers, also examined this, and found that residual variance and beta were both relevant in explaining cross-sectional returns.
 Note that the CAPM theory
had hardly been tested. Indeed, its main empirical application had assumed it
was true, and tested merely the persistence of mutual funds. But, given the
logic, and the fact that Lorie and Fischer showed what appeared to be a strong,
positive risk premium, there really was no alternative. In September 1971 Institutional
Investor had a cover story on the CAPM, “The Beta Cult! The New Way to
Measure Risk.” The magazine noted that investment managers were now “tossing
betas around with the abandon of Ph.D.s in statistical theory.” Unlike the
theory of efficient markets, the theory of asset pricing and risk has been
popular from its inception.
Note that the CAPM theory
had hardly been tested. Indeed, its main empirical application had assumed it
was true, and tested merely the persistence of mutual funds. But, given the
logic, and the fact that Lorie and Fischer showed what appeared to be a strong,
positive risk premium, there really was no alternative. In September 1971 Institutional
Investor had a cover story on the CAPM, “The Beta Cult! The New Way to
Measure Risk.” The magazine noted that investment managers were now “tossing
betas around with the abandon of Ph.D.s in statistical theory.” Unlike the
theory of efficient markets, the theory of asset pricing and risk has been
popular from its inception.
When scientists anticipate empirical confirmation just around the corner, as they did in 1970, they are really much further than they realize. Again and again, the idea is that if a bunch of smart people apply themselves to a problem that did not previously have a lot of specific attention, it is only a matter of time before it will be solved. That the initial tests of the CAPM were not very supportive, was presumably just a data problem, though with hindsight they were as doomed because we now know it is empirically untrue.
Merton Miller and Myron Scholes (1972), two economists who would later win the Nobel Prize for independent theoretical work, pointed out several flaws in Douglas’s empirical work. The important point to remember is that any empirical test is incomplete. That is one does not test theories and reject them; in practice, testers tend to publish only tests that are consistent with their prior beliefs because they sincerely believe that to do otherwise would be a mistake. Scientists know that posterity belongs, not to the humble and virtuous, but for early discoverers of important truths. Thus, if you know the truth, as a scientist, your goal is to get published quickly proving that truth in some way so you can become one of the founding fathers.
Miller and Scholes found Douglas’s effect was greatly diminished by controlling for potential biases caused by
- Changing interest rates
- Changes in volatility
- Measurement errors in beta
- Correlations between residual volatility and beta
- An inadequate proxy for the market
- Cross-sectional correlation in residual errors
- Correlation between skewness and volatility
Taking these issues into account diminished but did not eliminate Douglas’s findings. It was inevitable that controlling for so many things diminishes any effect, because the more degrees of freedom you add to an explanation, they more you spread the effect among several variables as opposed to one.
Then, the seminal confirmations of the CAPM were provided by two works, Black, Jensen and Scholes (1972), and Fama and MacBeth (1973). They both applied the following “errors in variables” correction to Douglas. They formed portfolios on the basis of earlier estimations of beta, and then estimated the beta of the resulting portfolios. This would reduce the problem that plagued the earlier tests, because previously a high beta stock (for example, beta = 2) would, on average, be overestimated. That is, if betas are normally distributed with a mean of 1.0, and measured betas are simply the true betas plus error, the highest measured betas will on average have positive errors. So, a stock with a measured beta of 2, on average has a true beta significantly lower, say 1.75. On the other side, lower-than-average estimated betas would have forward betas that were closer to 1.0, so a 0.4 estimated beta would probably be closer to 1, like 0.6, in practice.
So, grouping into portfolios based on prior betas, then create portfolios based on those sorts, and measure beta, diminishes the errors in variables problem.
The two-pass tests were of the form:
![]()
Run on the portfolios created via the prior betas, and then on the second pass
![]()
and looking at the stock returns, they found the predicted result: higher beta correlated with higher returns. Even more important, idiosyncratic volatility of these portfolios was insignificant.
Figure 2.1
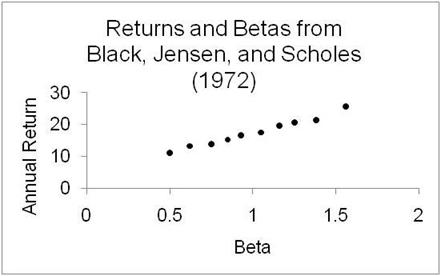
For both Black, Jensen, and Scholes and Fama-MacBeth, the slopes were positive—higher beta, higher return—which was all everyone interested needed to know. The only mild concern was the slope, which seemed a little flatter than anticipated. For example, in Fama and MacBeth, the hypothesis that beta is uncorrelated with returns is significant only for the entire 1935-to-1968 sample; in each of the 10-year subperiods you could not reject the hypothesis that there was no effect between beta and returns.
In spite of lukewarm support, these tests had staying incredible staying power as references that the CAPM worked. The tests were not corroborated, merely cited again and again over the next few decades. Even in the 1990s popular finance textbooks cited these original tests as the primary evidence of the CAPM’s validity.
For a few decades all was right in the world. The CAPM was slick financial theory, mathematically grounded, and empirically relevant.
But notice that the major perceived flaw in Douglas’s initial work was correcting for estimation error in beta. This problem should bias both residual volatility and beta similarly, yet in Douglas’s work, residual risk was significant, while beta was not. The error-in-variables correction reversed this. With the benefit of hindsight, this is totally explainable. Both beta and residual variance are positively correlated with size, a stock characteristic subsequently found highly correlated with returns. Both Black, Jensen, and Scholes and Fama-MacBeth created portfolios based on initial sorts by estimates of beta, so that the resulting spread in average beta would be maximized. But this then makes the size effect show up in the betas, because sorting by beta is, in effect, sorting by size. They could have presorted by residual variance, which is also correlated with size, and the results would have been the same as found for beta, only with residual variance the explainer of returns. Presorting by betas made the spread in betas large relative to the residual variance spread, and so made the small cap effect to speak through beta, not residual variance.
Of course, that is all with hindsight, knowledge of how the size effect works, before all the work in the 1980s showing how to correct for various biases that exaggerated the size effect. Nonetheless, it was somewhat inevitable that a theory, touted as the Next Big Thing before its first real test, given limited computing ability, is tested until the right answer is generated, and everyone stops making corrections, and cites the articles prominently for the next 20 years. As we subsequently learned, there were many more corrections to make (for example, most of the size effect was measurement error), but with the right results, there was little demand for such scrutiny. In general, we test results with reasonable thoroughness, where reasonable is influenced by the plausibility of our result.
Around 1980, Merrill Lynch printed large beta books, showing the beta for every stock. In 1990, William Sharpe, and Harry Markowitz won the Nobel Prize for their work in developing the MPT, which the Nobel Committee considered to be the “backbone of modern price theory for financial markets.”
The Beginning of the End of CAPM
The initial tests in the early 1970s were positive, yet more like Keynesian economics than any theory of physics: it had a consensus one taught to students, but was also empirically dubious to anyone in the know, and practitioners generally ignored it.
One of the early issues was technical in nature, having to do with sequentially estimating betas and returns. A big part of this was mere computing power. Before 1980, running a regression was difficult and running Maximum Likelihood functions nearly impossible. These more complex functions, which are a mainstay of empirical research today, use a hill-climbing algorithm that involves a lot of steps. It is not a closed-form solution that involves a fixed set of steps as in matrix algebra in Ordinary Least Squares. So, researchers satisficed with empirical work more primitive than anything one can do today in an Excel spreadsheet. Once computing got cheap, people tended to look again at early empirical work and found it could be improved by more modern techniques that were superior.
A maximum likelihood approach avoided several technical problems in BJS and F&M by simultaneously estimating betas, intercepts, and slopes. Shanken (1985) , Gibbons (1982), and Gibbons, Ross, and Shanken (1989) rectified several technical issues in BJS and F&M, testing the heart of the CAPM by whether or not the market is mean-variance efficient (as implied by Tobin and Sharpe). They applied Wald, Maximum Likelihood, and Lagrange Multiplier tests, as if this mélange is better than just one test. While Shanken and Gibbons rejected the CAPM at the 0.1 percent level, no one really cared about the substance of their results, because given any sufficiently powerful test, all theories are wrong. The CAPM was never considered seriously flawed via these investigators. For example, Newton’s ideas don’t work if we measure things to the tenth decimal place, but they still work. Powerful tests on whether the CAPM was true were publishable, but everyone knew it was an almost impossibly stern standard. Such findings were published in the top journals, but I doubt anyone was convinced as to the CAPMs’ practical value through these tests.
Roll proved that any mean-variance efficient portfolio would necessarily be linearly related to stock returns given investors are risk averse. It implied that to the CAPM’s main implication, therefore, was merely whether or not the market was mean-variance efficient. Roll then added, given the relevance of the present value of labor income and real estate in a person’s portfolio, the stock market was clearly not the market, clearly not mean-variance efficient, and therefore the CAPM was untestable. When the CAPM was being sullied in the 1990s, Roll and Ross (1994) and Kandel and Stambaugh (1996) resurrected this argument and addressed the issue of to what degree an inefficient portfolio can generate a zero beta-return correlation, which by then was accepted as fact. That is, is it possible that beta is uncorrelated with the S&P500 or whatever index is being used, even though it works perfectly with the true market index? In Roll and Ross’s words, if you mismeasure the expected return of the market index by 0.22 percent (easily 10 percent of one standard deviation away), it could imply a measured zero correlation with the market return.
This sounds devastating to tests purporting to reject the CAPM, but to generate such a null result with an almost efficient index proxy, one needs many negative correlations among assets, and lots of returns that are one hundred fold the volatility of other assets. In other words, a very efficient, but not perfectly efficient, market proxy can make beta meaningless—but only in a bizarre world where many stocks have 100 times the volatility of other stocks, and correlations are frequently negative. Now average stock volatilities range from 10 percent to 300 percent, most between 20 percent and 60 percent annualized. Betas, prospectively, as a practical matter, are never negative for stocks that are not explicit short portfolios (eg, the ProShares short ETFs).
It is fun to prove that there exists an equilibrium where, say, raising prices leads to more demand (a giffen good), or where greater individual savings lowers aggregate savings (the paradox of thrift), or where protecting infant industries increases domestic productivity. These are all possible scenarios, and you can prove them rigorously given various assumptions, but they are generally untrue, empirically counterfactual. The fact that the market is not mean-variance efficient could imply a zero beta-expected return, cross-sectional relationship, but this would be highly implausible because it would imply many large negative correlations between stocks.
As a practical matter, Shanken (1987) found that as long as the proxy between the true market was above 70 percent, then rejecting the measured market portfolio would also imply rejecting the true market portfolio. So if you thought the market index, any one of them, was highly correlated with the true market, the CAPM was testable as a practical matter.
The big counterfactuals to the CAPM were two anomalies discovered around 1980: the size anomaly and the value anomaly. Small cap (that is, low market capitalization) stocks had higher returns than large stocks, while value stocks (aka, low price-to-earnings, high book value-to-market value, high dividend ratios) outperformed their opposite. Black, Jensen, and Scholes reported beta deciles with returns that had about a 12 percent annualized difference between the highest and lowest beta stocks. But for size, estimates of the difference in returns between the bottom and top size deciles was an eye-popping 15 to 24 percent.
Figure 2.2
The Original Size Effect
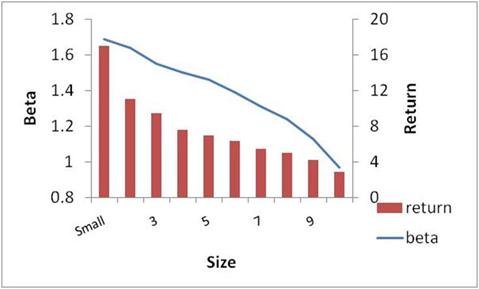
While the betas were positively correlated with size, that was insufficient to explain this big return differential. Something very strange was going on, and it started the hornets’ nest buzzing. Within a year of the finding of the size effect, there was a special issue in the Journal of Financial Economics on this issue.
Over the next decade, several adjustments were made, and the size effect was drastically reduced, down from initial estimates of 15 to 24 percent to around 3 percent, annually, for the difference between the smallest and lowest capitalization stocks. Many of the biases were technical, but no less real, and affect many historical findings. The first tip-off that something was rotten in the size effect was that 50 percent of it was in January, 25 percent in the first five days of the year. What economic risk factor is so seasonal? What was to become known as the January Effect, where small stocks outperformed large stocks in the month of January, was soon found to be highly influenced by the error caused by averaging daily returns. For example, if you average daily returns, and add them up, you get a very different result from if you cumulate daily returns, and average them. If you have a very small cap stock, and its price moves from, say, its bid of 0.5 to its ask of 1.0 and back again, every day, its arithmetic return is thus +100 percent, –50 percent, +100 percent, and –50 percent, for an average daily return of 25 percent. But in reality, its return is zero, which you would get by taking the geometric sum and dividing by the number of days. Averaging daily return for a portfolio assumes one is rebalancing a portfolio to equal-weighted starting values every day, highly impractical given one generally buys at the ask (high), and sells at the bid (lower). This arithmetic averaging issue arises quite a bit in finance. Blume and Stambaugh (1983) found this bias cut the size effect in half.
Another big technical adjustment was discovered by Tyler Shumway (1999), who noted that delisted stocks often have “N/A” on the month they delist, and these delisting months are actually quite devastating: down 55 percent on average! As small stocks delist much more frequently than large stocks, this bias overstates the return on small stock portfolios. Delisted stocks tend to overstate their actual returns because they systematically do not state these large, negative returns when they leave the database used by most researchers. The effect was almost 50 percent of the size premium. The current effect of the size effect is now around 3 percent, and even that is driven by outliers, in that if one excludes the extreme, 1 percent movers, it goes away completely.
Size is clearly a correlated grouping, a factor, in that small cap companies are more correlated with one another than large cap companies. Many investment portfolios now make distinctions for size (micro cap, small cap, and large cap), which initially was thought to generate a big return premium, but now, it’s more classic diversification as opposed to easy money. But the return premium for the smallest cap group is only a couple of percent per year, an order of magnitude lower than what was originally discovered around 1980. The key question today is whether this factor is a true risk factor—something priced by the market, with special correlations—or whether it is survivorship bias in an unconscious research fishing expedition or possible a return premium from behavior biases (a “small stock aversion” effect).
In contrast, the value effect is considered stronger than the size effect, though its discovery was much less auspicious. Initial estimates by Basu (1977) estimated that the low price-to-earnings (aka P/E) stocks outperformed the highest quintile P/E stocks by 6 percent annually, which is close to the current estimate of what the premium to a value over growth portfolio should be.
Figure 2.3
The Original Value Effect

Subsequent work played on this factor in various guises. Bhandari (1988) found that high debt-equity ratios (book value of debt over the market value of equity, a measure of leverage) are associated with returns that are too high relative to their market betas. Stattman (1980) documented that stocks with high book-to-market equity ratios (B/M, the ratio of the book value of a common stock to its market value) have high average returns that are not captured by their betas. P/E, book/market, and dividend yield are all highly correlated ratios that relate a market price to some metric of fundamental value, such as book value or earnings. For some reason, the beat-up stocks, those with low earnings but even lower prices, tend to outperform. Unlike the size effect, this was not concentrated in January. Though never as popular as the size effect in the 1980’s, the value effect has been more successful than the size effect over the past 30 years (size-oriented funds were started in the 1980s, while value and growth funds became popular only in the 1990s).
The data on the equity premium, size effect, and value effect, are generally considered to create positive premiums. The ‘Small minus Big’ category cross tabs between high and low book/market, to abstract from this effect ‘value’ effect. Similarly, the ‘High minus low’ category is cross-tabbed between the size groupings. Note that the value effect actually grew since initially discovered, highlighting why the value/growth distinction has grown in popularity (unlike effects like ‘low price’, which have evaporated). While both the size and value effects are smaller than when initially discovered, there are still there. These results abstract from all sorts of costs in implementation (commissions, taxes, an internal rate of return that accounts for flows in and out of these classifications, etc), so their economic significance is not obvious, but they remain intriguing.
Table 2.1
Total Return to Fama French Anomalies/Factors
1926-June 2010
Market-Rf Small Minus Big High Minus Low
1926-1980 6.30% 2.98% 3.78%
1981-2010 4.31% 1.03% 4.88%
Data from Kenneth French’s website
Bill Schwert (1983) wrote in a review of the size effect: “I believe that the ‘size effect’ will join the ‘weekend effect’ . . . as an empirical anomaly,” highlighting the confusing nature of popular anomalies. The weekend effect was part of the collection of seasonal anomalies very prominent in the early 1980s. There is the January effect, whereby small stocks outperform large stocks, the September effect (the worst month of the year), the Monday effect (worst day of the year), the Friday effect (best day of the week), and the belief that days before holidays tend to be good. In the mid-1980s, Werner De Bondt and Richard Thaler (1985, 1987) got a lot of mileage out of their documentation of mean reversion in stock prices over period of three years—this finding was essentially reversed a decade later through a much stronger momentum effect over one year, and there has been very little corroboration of the three-year reversal finding. Fischer Black (1995) remarked that “I find theory to be far more powerful than data,” after being burned in this field by false leads so many times, and Bill Sharpe noted that “I have concluded that I may never see an empirical result that will convince me that it disconfirms any theory” (Bernstein, 2005). Understandable, but there’s an unhealthy nihilism there.
The weekend effect, like the other seasonal anomalies, disappeared like the latest miracle diet. Thus it is understandable that the latest anomaly is treated skeptically by your average expert for good reason, because most are dead ends based on selection biases and just bad data.
APT Tests
In the 1970s, before the full development of the Arbitrage Pricing Theory, Barr Rosenberg (1974) suggested that portfolios demarcated by firm characteristics could likely serve as factors. Tests of the APT started in the Eighties, many pointing to the Roll critique in that the APT is inherently more susceptible to empirical validation than the CAPM, but the APT and the SDF both gave sufficient justification for doing the same thing, basically, to find some time series and use that to explain returns. If you think of the time series of stock returns, you merely need a set of equivalent time series to regress this against. But the basic approach has three distinct alternatives: the macro factor approach (oil, dollar, S&P500), the characteristic approach (size, value), and the latent factor approach (statistical constructs based on factor analysis).
In 1986, an initial test of the APT by Chen, Roll, and Ross seemed to show that the APT worked pretty well using some obvious macroeconomic factors. They used the factors representing Industrial Production, the yield between low and high risk bonds (actually, between BBB and AAA bonds, which are both pretty low risk), between short- and long-term bonds (the slope of the yield curve), unanticipated inflation, expected inflation, and finally, the market (as in the simple CAPM). These were all reasonable variables to try because they were all correlated with either the yield curve, or things investors care about. Now, given that Ross was the creator of this model, it should come as no surprise that they found these factors explained a lot of return variation. But only a few factors seemed priced, that is, you may find that stocks are highly correlated with a factor, such as the market, but on average stocks with a greater loading on this factor did not generate higher returns, the risk premium or the price of risk may be zero. This is what we mean when we say some risks are not priced (common risks that are not priced include industry risk, which clearly affects sets of stocks, though on average no industry, by itself, generates superior returns).
While this finding was promising, it was not a lot better than the CAPM in regard to its ability to explain returns, and did not explain the perplexing value or size anomalies that were confounding academics in the 1980s. More troublingly, in future tests of the APT, no one championed any particular set of factors, except as a comparison, so you have people comparing an APT test using oil, employment growth, and the S&P, and another using the dollar, investment growth, and corporate spreads. As novelty is a big part of getting published, and there were no restrictions on what is allowed, the multiplicity of models examined in the literature was inevitable.
While the Chen, Roll, and Ross approach was intuitive—you could understand the factors they were suggesting—a new approach was being forged that seemed even more promising: The idea that risk factors were statistical constructs, called latent factors, because they were latent, not clearly identifiable by words. These are very statistical constructs that appealed to finance professors familiar with the matrix mathematics of eigenvectors and eigenvalues, a branch of mathematics that is both deep and has proven quite practical in other applications.
If we think about the original mean-variance objective of investors, the latent factor approach actually makes the most sense. If one is minimizing portfolio volatility and cross-sectional volatility comes from several factors, all significant factors need to be addressed. One could come up with intuitive factors that span this space, but there are mathematical methods that are more powerful than mere intuition. Yet the first factor, which explains about 90 percent of the total factor variance, is about 99 percent correlated with the equal-weighted stock index (Connor and Koraczyk, 2008). This alone suggests that latent factors were not going to be a good alternative. Consider that many researchers use either the value or equal weighted index as proxies for the market, both using eminently reasonable justification. For example, the value-weighted market proxy was used as the market by some researchers (e.g., Fama and French 1993, 1995), Jegadeesh and Titman (993), while others used the equal-weighted market (Chopra, Lakonishok and Ritter 1992, Jones 1993), and some used both (Kothari, Shanken and Sloan 1995). You can argue the value-weighted proxy is more like the market because it weights stocks by their actual dollar size, giving more weight to Microsoft than some $50 million Internet start-up from Utah. On the other hand, the equal-weighted proxy weighs small firms more, and these firms might be more representative of smaller, unlisted companies that make up the true market portfolio. The bottom line is, if either worked considerably better, we would have a story for why it should be the market proxy, and researchers would have stuck with one over the other. Neither works better than the other (their betas do not explain average returns) so it really doesn’t matter. Now, if 90 percent of the latent factor approach is indistinguishable in power to the CAPM, and there isn’t a big difference between the value- and equal-weighted index, it is improbable the APT would bear fruit.
But even if the latent factor approach was empirically successful, it has another large problem. Most researchers assumed there were around three to five factors, all declining rapidly in statistical relevance. But while factor 1 looked a lot like the equal-weighted index, the other factors were not intuitive at all. Furthermore, many stocks had negative loadings on these secondary factors, so whereas the loading on the first factor, as in the CAPM, were almost all positive, these other strange factors, with no intuition, had 60 percent with positive loadings, and 40 percent with negative loadings. You could not explain exactly what the factor was, but sometimes it generated a risk premium, sometimes you were presumably paying for its insurance like properties—even though no one had enough intuition to figure out what this provided insurance against. Consider a broker suggesting that a stock is a good addition to the portfolio because it has a negative loading on the third factor, which no one really knows what it is, but one should be eager to earn 1 percent less because it will pay off big in some scenario when this is valuable. I am certain that this sales pitch has never happened, and considering that asset pricing theory is based on the assumption that people are in generally investing this way, is cause for skepticism.
Empirically, both of these APT approaches generated at most a modest improvement to the CAPM, and a slightly better ability to explain the perplexing size effect. Generally, if something is true and in the data, someone will find it, and the APT was a license to throw the kitchen sink at returns. It was rather surprising that this approach was so unfruitful given its degrees of freedom.
Fama and French Put a Fork in the CAPM
The debate changed dramatically when Fama and French published their paper in 1992. The key finding was not so much showing value and size generate large returns in the U.S. data, it was in showing that whatever success beta had, it was completely explained by the size effect. “Our tests do not support the central production of the [CAPM], that average stock returns are positively related to beta.” That is, if you remember the earlier graph from section 2, now we have Figure 2.4.
Figure 2.4

Shanken and Gibbons proved the CAPM wasn’t perfect, which really was not that important, because nothing is perfect. Fama and French showed it was not even useful. It’s not even an approximation; it’s not insufficiently linear, or insufficiently positive, its point estimate has the wrong sign! Stephen Ross (1993) noted that in practice “the long-run average return on the stock, however, will not be higher or lower simply because it has a higher or lower beta.” The previous single measure of expected return was accepted now as not being useful even as an incomplete measure of risk.
Such an empirical rejection would seem to be fatal, but this highlights the non-Popperian nature of real science. In Karl Popper’s construct, theories produce falsifiable hypotheses. If these hypotheses are falsified, the theory is then rejected. The CAPM predicted that beta was linearly and positively related to stock returns: the actual slope was zero. End of story? It would be naïve to think that after 25 years, a simple fact would cause so many finance professors to abandon an idea that was the backbone of their research papers, and formed the basis for lectures they had given for a decade, would be snuffed out like runt on a farm. In Thomas Kuhn’s paradigms, researchers see the seminal anomaly explained with a new theory, and then create a new theory in the new paradigm. But the Fama-French approach was clearly a “mend, don’t end” approach to the CAPM. The paradigm would continue, just as the APT (or SDF), but now, a three-factor model, the now ubiquitous three-factor F-F model
![]()
Note that this approach is really
just the CAPM equation with two extra terms. The first term, ![]() , is the return on the market above the
risk-free rate, and this, plus the risk-free rate, is the CAPM. The next term,
, is the return on the market above the
risk-free rate, and this, plus the risk-free rate, is the CAPM. The next term,
![]() , is the return on the small cap portfolio
minus the big cap portfolio. As small cap firms outperform big cap companies,
this average is positive, suggesting this has a positive price, that is, it is
a priced-risk factor. The loading on this factor, bsize, represents the sensitivity of an asset to this
factor, as measured by the beta on this factor from a regression. The final
term,
, is the return on the small cap portfolio
minus the big cap portfolio. As small cap firms outperform big cap companies,
this average is positive, suggesting this has a positive price, that is, it is
a priced-risk factor. The loading on this factor, bsize, represents the sensitivity of an asset to this
factor, as measured by the beta on this factor from a regression. The final
term, ![]() , is the return on the high book to
market (aka value companies, low P/E companies) portfolio minus the return on
the low book to market (aka growth companies, high P/E companies).
, is the return on the high book to
market (aka value companies, low P/E companies) portfolio minus the return on
the low book to market (aka growth companies, high P/E companies).
This approach is totally consistent with the APT and SDF, in that either of these motivate the addition of the value and size factors as risk factors, because they are factors that explain a lot of cross-sectional volatility and they are on average positive, suggesting they are priced and thus reflect some state variable that affects our utility. Working backward, since only risk generates average returns, the anomalies imply some kind of risk. As the APT says, it really does not matter what or where these factors came from, all that matters is they must be priced linearly, and so the beta terms representing their loading tell us how much of these factors are being used. This is known as atheoretical risk factor identification, because it comes from returns, not something more basic. The Kuhnian paradigm was not shifted; an epicycle was added.
Saving the Standard Model
Generally, better empirical data and testing generates greater support for the correct theory over its incorrect rival. Correct theories get clearer as the data refine them. In the case of finance, the data has spawned the correlate to superstring’s multiple universes (now, 10500 potential solutions), and the past is unconsciously rewritten so that a young researcher would think there has been a consistent, asymptotic trend toward the truth.
Currently, the three-factor Fama-French model remains perhaps the most popular model for benchmarking equity returns by academics, although it has a significant number of detractors. The main puzzle to the Fama-French model is what kind of risk factors do the value and size represent? Small stocks have higher betas, and are more volatile, but as these characteristics themselves are not positively correlated with returns, we can’t say that small stocks outperform large stocks because of their volatility, or covariance with the market. Value stocks, actually have betas that are higher in booms, and lower in busts, suggesting a win-win approach to investing that is decidedly not risky. So in what way are small size, and high-book-to-market (low P/E) stocks risky?
Early on in the size effect, people were at a loss to figure out what kind of risk that size, outside of beta, captured. Remember, the obvious risk, residual risk from these very small stocks, was diversifiable, and so not risk. Fama and French came upon the idea that both the value premium and the small stock premium were related to some sort of distress factor, that is, value stocks, whose price was beaten down by pessimists, and small stocks, which had less access to capital markets, probably had more risk of defaulting, or going bust, if the economy faltered. It may not show up in correlations or covariances, but that’s merely because such risks are very episodic, like the risk of a heart attack: The first symptom of a heart attack is a heart attack.
There were two problems with this interpretation. First, as Daniel and Titman (1998) documented, it was the characteristic, rather than the factor, that generated the value and size effects. They did an ingenious study in that they took all the small stocks, and then separated them into those stocks that were correlated with the statistical size factor Fama and French constructed, and those that were not. That is, of all the small stocks, some were merely small, and weren’t correlated with the size factor of Fama-French, and the same is true for some high book-to-market stocks. Remember, in risk it is only the covariance of a stock to some factor that counts. Daniel and Titman found that the pure characteristic of being small, or having a high book-to-market ratio, was sufficient to generate the return anomaly, totally independent of their loading on the factor proxy. In the APT or SDF, the covariance in the return with something is what makes it risky. In practice, it is the mere characteristic that generates the return lift. Fama, French, and Davis (2000) shot back that their approach did work better on the early, smaller sample, and more survivorship biased 1933-to-1960 period, but that implies at best that size and value seem the essence of characteristics, not factors, over the more recent and better documented 1963-to-2000 period. In a similar vein, Todd Houge and Tim Loughran (2006) find mutual funds with the highest loadings on the value factor reported no return premium over the same 1975-to-2002 period, even though the value factor generated a 6.2 percent average annual return over the same period. Loading on the factor, per se, did not generate a return premium.
This suggests that size and value are not risk factors, just characteristics correlated with high stock returns cross-sectionally. This could be an accident of historical data mining, as when people find that some county in some state always votes for the correct president, which is inevitable given a large sample, but ultimately meaningless. Alternatively, these findings could be proxies for overreaction. People sell small stocks too much, sell value stocks too much, and a low price leads to them to being both small cap and having a high book-to-market ratio. But this overshoot sows the seeds for an eventual correction. This effect works the opposite way for large cap and low book-to-market ratio stocks, where the prices shoot too high. Lakonishok, Shleifer, and Vishny (1994) proposed just such a model, and this is the standard behaviorist interpretation of the size and value effect: They capture systematic biases, specifically, our tendency to extrapolate trends too much to ignore the reversion to the mean.
Another problem with the distress risk story was that, when you measure distress directly, as opposed to inferring it from size or book value, these distressed stocks have delivered anomalously low returns, patently inconsistent with value and size effects as compensation for the risk of financial distress. Around 2000, when I was working for Moody’s, I found this to be true using Moody’s proprietary ratings data. Moody’s had a unique, large historical database of credit quality going back to 1980, and I found that if you formed stock portfolios based on the credit rating of the equity’s debt, there was a perfect relationship from 1975 to 2000: the lowest-rated credits (C) had the lowest returns, followed by the next lowest-rated companies (B), then Ba, and so on, to AAA with the highest return. Better credit and lower default risk implied higher future stock returns.
Ilya Dichev had documented this back in 1998, but this finding could be brushed off because he presumably had a poor default model (he used the Altman Model). But then several others documented a similar result, and finally Campbell, Hilscher, and Szilagyi (2006) find the distress factor can hardly explain the size and book or market factors; in fact, it merely creates another anomaly because the returns are significantly in the wrong direction (Agarwal and Taffler (2003), Grifffin and Lemmon (2002), Vassalou and Xing (2004)). Distressed firms have much higher volatility, market betas, and loadings on value and small cap risk factors than stocks with a low risk of failure; furthermore, they have much worse performance in recessions (Opler and Titman 1995). These patterns hold in all size quintiles but are particularly strong in smaller stocks. Distress was not a risk factor that generated a return premium, as suggested by theory, but rather a symptom of a high default rate, high bond and equity volatility, high bond and equity beta, and low equity return.
Finally, there is the issue of what the market is doing in the three-factor model. That is, why include the market if it does not explain equity returns? Simple, Fama and French respond, because if you also include government bonds, you need the market factor to explain why the stock indexes appear to rise more than bonds do, because it is not like the factors for size and value—whatever they represent—that can explain the aggregate difference in return between stocks and equities. The market factor, which Fama and French admit is not relevant for distinguishing within equities, is necessary to distinguish between equities as a whole and bonds. And so it is with most models, as currency models find factors built off such proxy portfolios that help explain the returns on various currencies, but they only work in explaining currency returns. The same holds for yield curve models, where risk models are a function of those points on the yield curve that generate positive expected returns, and thus explain the yield curve by way of this risk factor. None of these factors apply outside their parochial asset class, though; they just explain themselves. If these were truly risk factors, and represented things that paid off in bad states of the world, it should hold across and within all asset classes, so that, say, a set of risk factors used to explain, say, equities, would be applicable toward currencies and the yield curve.
In the end, we have atheoretical risk factors, each of which was chosen to solve a parochial problem recursively, so that return is a function of risk, which is a function of return. Value and size, longstanding anomalies, were simply rechristened as risk factors, and then used to explain, well, themselves. Fama and French said it worked out of sample by testing it on strategies sorted by P/E ratios, but the P/E ratio is so correlated with the B/M ratio that this is hardly an out-of-sample confirmation. Furthermore, the inability of the market to explain cross-sectional returns of stocks within the market, did not hurts its importance in explaining why the market explains the differential return between it and the bond market, even though, again, this is tautological: The higher return of equities over bonds is explained by the return of equities over bonds. If it is a risk factor, why does it apply only to itself, that is, the market, and not to individual equities?
It did not take long for researchers to jump on this bandwagon. A new anomaly, momentum, discovered by Jegadeesh and Titman (1992), as past winners over the last 3 to 18 months tended to continue over the next 3 to 18 months. They did not even propose a risk motivation for this finding, and even Fama and French are reluctant to jump on that one, which would lay bare the factor fishing strategy at work. Mark Carhart (1997) was the first to then add momentum (a long winners–short losers portfolio) to the F-F three-factor model and create a four-factor model in a study. At the very least, it captured things that a naïve investor would make money on, which was useful in Carhart’s case because in examining mutual fund returns, to the extent a fund is relying on a simple strategy that rides on momentum, size, or value, it seems relevant to how much pure alpha they had (although one could argue that implementing a momentum strategy before academics discovered it involves alpha).
Serial Changes to APT
The striking fact about multifactor models applied to cross-sectional equities is that there is no consensus on the factors. The APT and SDF approaches have slightly different emphasis in empirical tests, and the APT testers generally have more intuitive results, whereas the SDF approach generates more statistically powerful, but less compelling results, but generally it all comes down to identifying factors and using them to explain returns. Which returns? Well, after Fama and French, everyone tried to correlate a model with the returns of portfolios that are created by cross-tabbing book-to-market and size, two characteristics that are historically related to returns for some reason. That is, each month, you sort stocks into quintiles by size, and then sort within each quintile by book or market. You get 25 portfolios after the 5 by 5 sort. Many of the proposed models seem to do a good job explaining these portfolio returns as well as the three-factor Fama-French model, but it is an embarrassment of riches. Reviewing the literature, there are many solutions to the Fama-French set of size-value return, but there is little convergence on this issue. This is especially true given the great variety of factor models that seem to work, many of which have very little in common with each other.
For example, Chen, Roll, and Ross (1986) assert six factors as the market return, inflation (expected and actual), industrial production, Baa-Aaa spread, and yield curve innovations; Sharpe (1992) suggests a 12-factor model, while Connor and Korajczyk (1993) argue there are “one to six” factors in U.S. equity markets using principal components analysis. Ravi Jagannathan and Zhenyu Wang (1993) assert human capital and the market portfolio are the two factors because a metric of human capital is needed to capture the total market; they later argue (1996) that time-varying betas can explain much of the failure in CAPM. Lettau and Ludvigson (2000) use the consumption-wealth ratio in a vector autoregressive model to explain cross-sectional returns. Jacobs and Kevin Wang (2001) argue idiosyncratic consumption risk and aggregate consumption risk; and Jagannathan and Yong Wang (2007) have year-over-year fourth quarter consumption growth. This research is vibrant and ongoing, but the diverse approaches extant suggest they have not begun to converge, even within the prolific Jagannathan/Wang community. The bottom line is that unlike the value, momentum, and size, no one has created an online index of these more abstract factors because they change so frequently; there is no single such factor that would be of interest to investors.
Skewness
The idea that people really like right skewed assets, like lottery tickets, options, and highly volatile stocks, nicely explains why these assets have low returns: they give us so much pleasure when they hit a ten-bagger, we are willing to forgive the fact that they are eating a hole in our net wealth. For example, Harvey and Siddique (2000) found that a firm’s marginal contribution to negative skew, coskewness, can do as well as the Fama-French three-factor model. Yet, the data seem fragile. They calculate skew using 60 months of data for each stock, and this biases the data set because it excludes about 40 percent of the sample. Ang, Chen, and Xing (2002) find that downside beta, which is like negative coskewness, is positively related to returns for all but the highly volatile stocks, where the correlation with returns is negative. Furthermore, value and small companies that have positive skewness, suggesting they should have lower-than-average equity returns. Thus, skewness may be at work, but as a general measure of risk, it is quite fragile.
However, if people got an extra premium for buying assets with the 'bad' skew, a leftward skew as in bonds, then bonds should have pretty good return premiums, and they don't. Risky currencies, which have a leftward skew, do not have a demonstrable premium above assets without this skew. Utility stocks have historically had leftward skew because their returns are capped via regulation, yet they have not outperformed the market since data has been kept.
Levy, Post, and van Vliet (2003) show that most of these skewness models that have investors caring about the beta and the third moment of their future returns imply an inverse S-shaped utility function with risk seeking beyond a return level. If concavity is imposed, then the annualized gamma premium is one-tenth of the basic equity risk premium in these models, hardly enough to explain the massive failure of the first-order factor. By contrast, if concavity is not imposed, the first order conditions of portfolio maximization suggest that the market portfolio is more likely to represent the global minimum portfolio, which is absurd.
Initial theoretical work by Rubinstein (1973) showed how one could add skewness and kurtosis with the CAPM. It has not yet generated a practical model, and not for a lack of interest. The Journal of Portfolio Management online list of abstracts mentions skewness in no fewer than 66 articles and kurtosis in 44.
Summary
The CAPM started with a tepid confirmation, and while there was much whistling past the graveyard, and hopes that warts like the size and value effect would go away, it turned out they merely focused researchers on questions they should have asked at the very beginning. The seeming correlation between beta and returns was mainly due to the correlation with the size effect, and this, in turn, was mainly due to measurement errors. Theoretical efforts in the 1970s and 80s focused on statistical tests that got around technical issues, as with issues of endogeneity and which risk factors are best, but ultimately the simple empirical anomalies discovered at that time (size and value) highlighted the shortcomings of the CAPM. The best cross-sectional predictor of equity returns is momentum and book-to-market, neither of which have an intuitive risk rationale. Tweaks to the model have been conspicuous in their ephemeral nature, always popping up in different guises.
The CAPM and its creators are still considered first-order intellectual achievements, in spite of the current thought leaders also describing it as being “empirically vacuous” (Fama and French, 2006) or that “having a low, middle or high beta does not matter; the expected return is the same” (Ross, 1993). Indeed, I would say the situation is worse, as volatility and beta are generally negatively correlated with returns.
Its extensions have proven equally impoverished. There’s clearly a greater truth at work in this case, the greater truth is that some asset pricing model will work, and it should have the neat CAPM properties of being linear in risk factors, not include residual risk, and include something very like the market as one of the prominent factors. The theory has little equal by way of praise from economists, who see the success of derivatives as proving the risk-reward portion of academic finance as manifestly fruitful. I doubt even Keynesianism had such high approval ratings at its apex. But the flaw of the CAPM isn’t that it is not perfect, but rather does not predict relative returns, even slightly, quite different from the flaws of Newtonian mechanics, which become apparent near the speed of light.
The golden age of the CAPM was from 1972 to 1992, from Fama’s initial confirmation of the theory to his rejection of it. Not that it ever really worked, or that portfolio managers ever mainly relied on beta in constructing portfolios. No, it was that among experts, the belief was that the CAPM was an innovation in our abstract understanding that would stand the test of time like Euclid’s Elements. Refined, extended, to be sure, but never junked. The concurrent development of the APT, and the general equilibrium SDF approach, were merely extensions. To the extent CAPM had difficulties; these more general approaches would fix them, but the basic ideas of the CAPM were paramount: linearity in pricing, and the positive premium of some systematic risk factors. It was further assumed that the main factor would be the market, and so a multifactor approach would merely add second order terms, in a very consistent way.
The shadow cast by the initial apparent success of the theory creates a strange longing for a time of order, even if that order was based on ignorance. John Cochrane wrote, the CAPM “proved stunningly successful in a quarter century of empirical work,” meaning it seemed to explain the data pretty well, until we found out this was merely due to beta picking up the size effect, which itself was mainly measurement errors. This longing for a prior sense of ignorance, when a popular theory appeared to be working, is a rather bizarre stance. It’s like saying how fun Christmas was when we believed in Santa Claus. True, but that’s harmless fun, not science.
Peter Bernstein wrote the best-seller Capital Ideas, which presents the modern finance architects as heroes and mavericks; one can almost hear the “Ride of the Valkyries” as one reads his firsthand account of their achievements. Even books that note the CAPM, or the APT, were empirically vacuous, paying homage to the standard theory in obligatory fashion; harping on its flaws was like criticizing Newton for not accounting for special relativity. Derivatives pioneer Mark Rubinstein’s 2002 homage to Markowitz noted that
“Near the end of his reign in 14 AD, the Roman emperor Augustus could boast that he had found Rome a city of brick and left it a city of marble. Markowitz can boast that he found the field of finance awash in the imprecision of English and left it with the scientific precision and insight made possible only by mathematics.”
Unfortunately, no Markowitzian model explains the sign, let alone the third digit, of asset returns.
In the words of leading research John Campbell, giving his overview of the state of finance at the Millennia, ‘Precisely because the conditions for the existence of a stochastic discount factor are so general, they place almost no restrictions on financial data ’. The effect of a good theory is to make an accurate view of the world less complicated, not more, but instead modern researchers focus on the framework’s potential as opposed to its predictive power. The stochastic discount factor approach encapsulating CAPM is surely not a coincidence to these researchers, it merely highlights that while currently wrong, it will be able to encompass the ultimate true theory.
The problem is, as the data have become clearer, the theory has become less clear. This is not a sign of a successful theory. Risk started out as merely volatility, and now volatile assets presumably have low risk through some spooky risk factor.
Last Section | Download PDF | Next Section