


The Creation of Risk Premiums and Asset Pricing Theory
The Creation of the risk premium paradigm that dominates finance is clearly not based on its empirical success. Outlining why it is so compelling necessitates going over the rather attractive logic used to derive its implications.
If the empirical data so clearly reject the risk premium theory, it begs the question as to why people believe it, as scientists are not stupid. The standard model has a mathematical beauty and unexpected consistency that makes it seem right, because something so beautiful must be real. Given its seemingly unimpeachable assumptions, it should work, but it doesn’t, which implies that one of the assumptions is wrong. This section outlines the creation of our current paradigm.
The story of risk is usually presented as the crowning success story of the social sciences, a manifestly human subject tamed through rigor and logic, with its cannon of heroes from Markowitz to recent Nobelist Danny Kahneman. As MIT economist Andrew Lo says, finance is ‘the only part of economics that works’, and within finance, risk rules (Bernstein, 2007). The story of risk was presented in a best seller by Peter Bernstein in Against the Odds: the Remarkable Story of Risk, where Bernstein chronicles the development of the Standard Model from the middle ages, and notes that:
“By showing the world how to understand risk, measure it, and weigh its consequences, they converted risk-taking into one of the prime catalysts that drives Western society. Like Prometheus, they defied the gods and probed the darkness in search of the light that converted the future from an enemy into an opportunity.” (Bernstein, 1998)
The Risk Premium starts with the ideas of Harry Markowitz and portfolio theory and the development of the Capital Asset Pricing Model (CAPM), what is called Modern Portfolio Theory, or MPT. If you can understand the CAPM, the extensions are straightforward, and these extensions form the Arbitrage Pricing Theory (APT) and finally to general equilibrium Stochastic Discount Factor (SDF) models, which represent the vanguard of current theoretical finance. The key concepts are risk aversion and diversification, which implies that certain systematic covariances are all that matter in this paradigm.
Prior to the CAPM, there was great confusion as to the essence of profits, which via division by the invested capital, is the same thing as the return on investment. The problem at that time was that, theoretically, profits should go to zero by way of competition, the same way arbitrage profits disappear in a market. Indeed, this was a major plank of Marx’s Das Capital, as the fall in profit would be one of the main spurs for the upcoming socialist revolution. Yet profits seemed to be a constant portion of national income, generating a true puzzle.
Prior the standard conception of risk, Paul Samuelson’s 1958 edition of his Economics textbook, had four types of reason given for why profits persist. First, it is just a return on capital, like the risk free rate is thought today, a function of the saving rate, time preference, and the productivity of investment. As ‘risk’ was not yet fully understood in modern terms, the distinction between the return on equity or Treasury bonds, could be conflated. That is, without some concept like beta, who’s to say equity is ‘riskier’ than Treasury bonds, and if so, so what?
Second, it could be a return to daring, but unforeseen innovation, Schumpeterian creative destruction. Profit is just the return to entrepreneurs. New technologies are introduced, and these drive growth and profit.
Third, there was Frank Knight’s view articulated in his treatise, Risk, Uncertainty, and Profits, which that the essence of profits was a return to uncertainty. In Knight’s view, ‘volatility’ was not related to profits because such risk can be diversified away. As he put it, “the busting of champagne bottles, if known to a precise probability, can be thought of as a fixed cost of storage. This is the principle of insurance.” (Knight, 1921, p. 213) Thus, to the extent volatility is calculable, it is not associated with a higher return, but rather merely a cost statistically amortized.
The only way people could make profits, in Knight’s view, was if something prevented capital from moving too quickly into profitable areas. The uncertainty that precluded easy entry by competitors, what generated otherwise abnormal profits, were ventures for which there is “no valid basis of any kind for classifying instances,” (Knight, 1921, p. 224) such as when an entrepreneur creates a new product. His conception of uncertainty has been hotly debated, as to whether the essence of how uncertainty inhibits capital may be due to moral hazard, the ability of the businessman to abuse the investor in such environments, a true uncertainty aversion, or something else. In any case, Knight sees businessmen making profits, by seizing on opportunities infused with uncertainty, as a subset of risk.
Lastly, there was the view that profits were monopoly returns. If competition is precluded via explicit law, or implicitly though some cartel, one can charge customers more than a marginal cost, and generate persistent profits.
All of these explanations of profits were rather unsatisfying. The monopoly profits explanation would be tenable if larger, more politically powerful companies generated higher returns over time, but while it has always been popular to lament the greater power of wealthy merchants, small stocks have done at least as well as large stocks since the data on these things began. Profits are greater than the risk free rate, so profits are not merely a ‘return to capital’. And return to ‘daring’ is really not an equilibrium: the boldness of an investment is not sufficient to generate a superior return, as most bold ideas are from cranks. Knight’s theory, meanwhile, was inherently difficult to apply because if you could measure it, it was not uncertainty. The idea of a risk premium filled a clear need, as the status quo was unsettled.
Currently, we see profits/investment as the return to bearing risk. It is positive in equilibrium because people do not like risk, and they hold it only in exchange for some premium return. The key pillars of the risk premium are twofold: diversification and decreasing marginal utility, the rest are details.
Utility Functions and Risk Aversion
Risk aversion applies to the assumption that people prefer a certain $1 to a 50% chance at $2 or $0, even though the latter has an expected value of $1. Risk is fundamentally related to something ‘we don’t like’ about uncertainty and this something is priced in financial marketplace because it cannot be eliminated, and people must be persuaded to tolerate it via a return premium. Thus we start with defining what, exactly, we don’t like about risk, and we begin with the the utility function.
Every advanced economics text starts with utility functions because economics is mainly about examining the implications of a bunch of individuals engaged in rational self-interest, where self-interest is defined tautologically as ‘that which maximizes their utility’. Thus, we need to know specifically what agents are maximizing. The concept of utility got its start as the solution to a thought experiments. A thought experiment is much more influential if the originator is a famous deep thinker, and Daniel Bernoulli was such a man, a Dutch mathematician who had family and made contributions of mathematics to mechanics as well as probability and statistics.
Bernoulli’s St. Peters Paradox was presented around 1738, an offered the following hypothetical. You pay a fixed fee to enter, and then a fair coin will be tossed repeatedly until a tail first appears, ending the game. The pot starts at 1 dollar and is doubled every time a head appears. You win whatever is in the pot after the game ends. Thus you win 1 dollar if a tail appears on the first toss, 2 dollars if on the second, 4 dollars if on the third, 8 dollars if on the fourth, etc. In short, you win 2k−1 dollars if the coin is tossed k times until the first tail appears.
How much would you be willing to pay to enter the game? The expected value of this game is infinity, because the probability of the payout is ½k, whereas the payout is 2k-1, meaning each scenario equals one half (½k × 2k-1=1/2).

This sum of infinite number of 0.5 diverges to infinity; "on average" you can expect to win an infinite amount of money when playing this game.
The St. Petersburg paradox is a situation where a naïve decision theory, which takes only the expected value into account, would recommend a valuation no rational person would presume, and can be resolved two ways. In one, it takes into account the finite resources of the participants. If your bettor has only $1000 to credibly apply to this bet, the expected value is about $9, not infinity. But even if you assumed you were betting against a hypothetically rich opponent, it seems ridiculous one would value this bet at infinity, and so a deeper solution seems intriguing. If we apply the notion of marginal utility, the payoffs are not proportional in utility, because receiving $1000 is not 1000 times better than winning $1, but rather much less. This diminishing marginal utility implies risk aversion, because the value of a payoff that returns 1000 or 0 with equal probability is not $500, but less.
Thus the concept of ‘utility’, which represents the amount of pleasure one gets from something, in units of ‘utils’. It seems that utility should be both increasing in the amount anything we have or consume, though increasing at a decreasing rate. In mathematical terms, the first derivative always positive, the second always negative. We always like more money but a dollar is worth less the more you have.
Over the next two centuries, utility functions became essential in economic analysis, and decreasing marginal utility was found to be a powerful assumption. It is assumed, not derived: the law of diminishing marginal utility is self-evident. After all, we like food less after eating a large meal, or have use for only a limited number of light bulbs after which they become totally useless. This became of fundamental importance when the Marginal Revolution in economics occurred 1862, as it was independently discovered by Stanley Jevons in England, Carl Menger in Austria, and Leon Walras in Switzerland. The really surprising and powerful thing about this theory was that it seemed very useful in explaining prices, especially because the marginal utility is the change in utility at the margin, a derivative, and economists love mathematics.
The chasm between economics pre and post Marginal Revolution is stark. Pre marginalism we didn’t have modern price theory. A bad assumption ruins a vast set of theories and their extensions, something that happens quite often (e.g., the labor theory of value). Post marginalism, prices are such that the marginal cost of something is equal to the marginal value (utility) for that same thing for any individual. That is, if you get $2 of utility from an ice-cream, you will consume ice cream until either the price rises above $2, or your marginal utility from ice-cream falls to $2. Without diminishing marginal returns, if you prefer your first ice cream at $2 cost, you would eat as much as you could afford, which would be a highly counterfactual implication. Given that people consume a variety of goods, it must be that they are all experiencing diminishing marginal returns to each good they consume, and reaching a multitude of satiation points where the amount of bread, shoes, houses, etc., are non-zero but also not the entire budget. The key information one needs in maximizing utility, or profits, are marginal: marginal costs (prices), marginal benefits (i.e., marginal utility for consumers, marginal revenue for producers). The ratio of price to the marginal utility per good is constant for everything in the household’s budget because if the ratio were any different on one item, you would not be maximizing your utility. The concept of utility, and diminishing returns as applied to something we consume, is central to economics because it is so powerful in explaining consumer behavior, and it is explained in one of the first chapters of every good microeconomics textbook.
In 1947 Johnny von Neumann and Oscar Morgenstern wrote The Theory of Games and Economic Behavior. von Neumann was a mathematician who had earlier tried to axiomatize set theory, and later the axiomatized quantum mechanics. Unfortunately, his work on set theory was made irrelevant by Godel’s Incompleteness Theorem, while his work in quantum mechanics turned out inferior to an approach developed by Paul Dirac, an approach that inspired Feynman to develop his popular path-integral approach to quantum field theory.
So when economist Oscar Morgenstern pulled him in to help write a book on two-person zero sum games like poker, von Neumann was the perfect person for generating assumptions that enable the construction of a formal system whose consistency and completeness can be rigorously proven. He created a set of axioms that defined how such players evaluated random payoffs that they would apply to their parochial problem of zero-sum games. The von Neumann-Morgenstern utility function incidentally became the most important contribution within the Theory of Games and Economic Behavior, the workhorse of economic models for the remainder of the century, because a modeler could count on them having consistent properties, rigorously proven.
The basics of the von Neumann-Morgenstern utility is that any normal set of preferences can be written as an expected utility. That is, a von Neumann-Morgenstern utility function for the case where there is a 40% chance of x1 and a 60% chance of x2, gives you an expected utility of
![]()
That is, you apply the probabilities to the utility of those states, not the utility to the probability times the state payoffs. All pretty simple, but the math that allows you to say this rigorously is difficult; it’s the kind of thing only an academic can appreciate, and a certain type at that. But it moved utility from focusing on a comparison of alternative consumption bundles, and their effects on utility now, but to a comparison of choices with risky outcomes which are functions of an unknown future.
Figure 1.1

Milton Friedman and Leonard J.
Savage (1948) used the von Neumann-Morgenstern utility function to introduce
the concept of univariate "risk aversion" which, intuitively, implies
that when facing choices with comparable returns, agents tend to choose the less-risky
alternative. Looking at the figure 1.1 above, we see that the average utility
of two equidistant payoffs generates lower utility ![]() that
the utility of the average payoff
that
the utility of the average payoff ![]() . You are happier to
get $50 with certainty than anticipating getting $0 or $100 with equal
probabilities, you prefer the sure-thing because of your risk aversion.
. You are happier to
get $50 with certainty than anticipating getting $0 or $100 with equal
probabilities, you prefer the sure-thing because of your risk aversion.
This is really just the St. Petersburg Paradox reasoning, but after the Marginal Revolution, the application of diminishing marginal returns via a von Neumann-Morgenstern utility function was seemingly much deeper, or more than just a thought experiment. The key is, an individual with diminishing marginal returns to wealth, a concave utility function is risk averse, and will undertake ‘risky’ investments if and only if the rate of return on risky assets exceeds the risk free alternative. Here ‘risky’ is defined as a non-sure thing, such as investing in the stock market, a lottery, or anything whose outcome has volatility. When one has diminishing marginal utility of wealth, given the same average (expected) wealth, the lottery with greater volatility is less preferred, because as the graph shows, a greater variance in outcomes leads to a lower expected utility for the same equal average payoff. This is a consequence of the diminishing marginal utility of wealth, and also seems eminently reasonable because by then it was central to microeconomics, and passes the sniff test intuitively: the poor have to appreciate a dollar more than the rich.
The implication of such a function is our common notion of risk aversion, because if utility as a function of wealth is increasing everywhere yet increasing at a lower rate, you prefer the certain expected value to the gamble of that same expected value. Arrow (1965) showed that a risky asset must have a higher return than the risk free rate, otherwise, no one would hold it, implying the market risk premium is greater than zero.
In practice economics uses the following to represent our utility for wealth:
![]() , or
, or ![]() ,
,
where W is our wealth, broadly defined, and a is the coefficient of risk aversion, and the higher a is, the greater the curvature of this function, and so the greater the risk aversion. These functions are all concave and increasing in W. Average estimates for a are usually between 1 and 3, not more than 10. You could include your present value of labor income or merely the cash in your wallet, but if we present value our life, and call it W, the idea is that a concave function of it is appropriate.
Within the expected-utility framework, the concavity of the utility-of-wealth function is necessary and sufficient to explain risk aversion. To repeat, diminishing marginal utility of absolute wealth is the sole explanation for risk aversion.
Diversification
The basic insights of Markowitz are intellectually satisfying because they at once so simple and intuitive, yet also mathematically complicated. The basic idea is ‘don’t put all your eggs in one basket.’ One can point to many esteemed premonitions of this advice, as when Solomon wrote, ‘Divide your portion to seven, or even to eight, for you do not know what misfortune may occur on the earth’ (Ecclesiates 11:2). Famed risk manager and author William Shakespeare, in The Merchant of Venice, Act I, Scene I, has Antonio say:
“…I thank my fortune for it,
My ventures are not in one bottom trusted,
Nor to one place; nor is my whole estate
Upon the fortune of this present year…”
Clearly the idea of diversification did not originate with Markowitz, but Markowitz proved how assets should not be viewed by themselves, but rather in the context of a portfolio, when one is ‘risk averse’ in the sense of Friedman and Savage. This contextual value is true of many goods: my computer is worth more because of useful software (compliment) and less because of my Blackberry (substitute). Similarly, investment assets have substitutes and compliments depending on the covariance of returns with other assets. Yet surprisingly, the context is not with me personally, but with a hyper-rational risk manager with infinite borrowing and lending ability. Given you take this rich, rational being as operative, Markowitz noted that idiosyncratic risk, risk unrelated to all the other assets, tends to disappear in a portfolio, leaving only systematic or non-diversifiable volatility, what was then considered risk. An investor who was risk averse would be trying to maximize returns while simultaneously minimizing variance.
The key to the portfolio approach is that the variance of the sum of two random variables is usually less than the sum of their variances, and never greater. Diversification is a rare free lunch in economics, in that you get lower risk merely by holding several assets instead of one, which is costless. As the number of stocks grows portfolio volatility asymptotes to some low, constant level.
Figure 1.2
Reduction in Volatility Via Diversification

In figure 1.2 above, the total volatility of a portfolio declines to a limit equal to the total systematic risk of the portfolio. This is because the diversifiable risk cancels out, but the systematic risk stays. Mathematically
![]()
Equation (1.4) above shows that as the number of assets N in the portfolio becomes large (e.g., >30), the only risk remaining is due to the covariances. If the covariances are on average zero, the portfolio variance goes to zero. Covariance is all that matters to a large portfolio. This is why the risks of a casino, where bettors are independently winning money from the house, generate pretty stable revenue to the house. The bettors will have uncorrelated, or zero covariance, to their payoffs, because card hands, or slot machine payouts, are independent. Thus a large casino has little risk from gambling payouts, excepting only when really large, but improbable payouts occur.
Markowitz created the now standard method of graphing a set of assets in volatility-return space, where volatility is on the x-axis, and return is on the y-axis (he later wished he had volatility on the y-axis, and I concur, but such is path dependence). There is a hyperbola around these assets that represent all the various combinations of each asset, with their various return and volatilities, and it curves because the covariance of the two assets makes their combination effect nonlinear. For example, in figure 1.3 below, the combinations of volatility and return for two correlated assets, A and B, is generated by the parabola. You can achieve any combination of total portfolio volatility by adjusting the relative proportions of A and B in the portfolio. Note that, trivially, if all the weight is on asset B, the volatility and return is equal to asset B, and the same would hold true for asset A. But when the weights are 50-50, the return is the arithmetic average, while the volatility is lower than the average. Portfolio volatility is not the simple average of the volatility of the constituent parts (actually very close to asset A), whereas portfolio expected returns are the simple average of the volatility of the constituent parts (right in the middle). Returns are additive, volatility is not.
![]()
Figure 1.3
The Volatility-Return Curve Generated From a Combination of Two Assets

The graph generalizes not merely to other assets, but other collections of assets, because collections of assets, portfolios, have simple mean, variance, and covariance characteristics too. Assume A and B are not assets, but rather portfolios of assets, or portfolios of portfolios of assets. The portfolios on the upper part of this curve are called ‘efficient portfolios’ because you cannot achieve higher return without adding to portfolio volatility. Much of Markowitz’s early writings involved a considerable amount of vector mathematics applied to statistics, mainly in outlining how to determine those portfolios on the efficient frontier, which given the complete set of assets in the universe, looks like the blue line below. In the days before cheap computing, analytical methods were very valuable, though now you can do it without much thought via optimization software totally orthogonal to Markowitz’s approach, making most of this work antiquated.
Figure 1.4

Harry Markowitz’s 1950 dissertation on the portfolio mathematics was to become the basis for his Nobel Prize in 1990. At the time the subject seemed to his dissertation advisor Milton Friedman, to contain a little bit too much statistics as opposed to economics, because it spent a lot of time on algorithms to determine the portfolio weights for the efficient frontier. Nothing stings like the lukewarm approval of men we respect, and so in a scene surely envied by many a thesis advisee, Markowitz noted in his Nobel lecture:
When I defended my dissertation as a student in the Economics Department of the University of Chicago, Professor Milton Friedman argued that portfolio theory was not Economics, and that they could not award me a Ph.D. degree in Economics for a dissertation which was not in Economics. I assume that he was only half serious, since they did award me the degree without long debate. As to the merits of his arguments, at this point I am quite willing to concede: at the time I defended my dissertation, portfolio theory was not part of Economics. But now it is. (Markowitz, 1990)
Markowitz’s early work was on the nuts and bolts of generating the efficient frontier, very statistical work without much intuition. It was understandable that Friedman found this focus of non-obvious relevance to economics, as with hindsight, the efficient frontier in return-standard deviation space has nothing to do with risk according to the new general equilibrium models. Markowitz’s big idea was merely equation 1.6, the power of diversification. So it is in economics where the seminal ideas are pretty simple when you know them, and as the vast majority of his work focused on particulars that were only of interest to other academics trying to get published and turned into a dead end, I think Friedman’s intuition has been vindicated. One could say that the efficient frontier underlies all portfolio mathematics, but really no more so than the idea that once a benchmark is chosen diversification is good, and Shakespeare knew that. The essence of their seminal insight is often available to many, and relatively terse, while the majority of their work is highly specialized, impressive, yet unimportant.
Primordial Extensions of Portfolio Theory.
In Markowitz’s 1959 book Portfolio Selection: Efficient Diversification of Investments, he discusses the following alternative measures of risk, as opposed to variance. These included standard deviation, expected loss, expected absolute deviation, probability of loss, and maximum loss.
Figure 1.5
Double Inflected Utility From Markowitz 1952

Kahneman and Tversky (1979) brought it back the inflected utility curve via prospect theory, but I think this will just prove Marx’s dictum that history repeats itself. Above is a utility graph from Harry Markowitz back in a 1952 JPE article, who was commenting on Milton Friedman and Savage's analysis in this same vein. It has the essence of prospect theory: risk loving for losses, risk aversion for gains, for some arbitrary wealth point. The profession dropped this thread because it was too rich: allowing people to be risk averse or loving, ignoring or overweighting small probability events, has not been useful in predicting behavior.
Another interesting extension that Markowitz addressed was the assumption of the normal, or the Gaussian, distribution. In 1962 Mandlebrot noted that asset returns were more heavily fat-tailed than Gaussian distributions (Mandlebrot 1962). The 1987 crash was a 27 standard deviation event highlights this point. While no one disputes that financial data are fatter-tailed than normal distributions, academics lost interest in this fact because what happens in terms of portfolio theory and models of risk and expected return works for Mandelbrot's stable distribution class, as well as for the normal distribution (which is in fact a member of the stable class). For passive investors, none of this matters, beyond being aware that outlier returns are more common than would be expected if return distributions were normal. Levy and Markowitz (1979) noted that mean-variance optimization is an excellent approximation to expected utility when not-normal.
Eugene Fama addresses this point in an interview on the Dimensional Fund Advisors:
“There was lots of interest in this issue for about ten years. Then academics lost interest. The reason is that most of what we do in terms of portfolio theory and models of risk and expected return works for Mandelbrot's stable distribution class, as well as for the normal distribution (which is in fact a member of the stable class). For passive investors, none of this matters, beyond being aware that outlier returns are more common than would be expected if return distributions were normal.” (see http://www.dimensional.com/famafrench/2009/03/qa-confidence-in-the-bell-curve.html#more).
Tobin’s Separation Theorem
Markowitz only looked at risky assets. James Tobin (1956) found that if you throw in one ‘safe’ asset with zero volatility, you get a neat result: the optimal portfolio in return-volatility space consists of one common portfolio representing all of the risky assets, and various proportions of the safe asset (i.e., a riskless Treasury bill). Tobin was a macroeconomist as opposed to a financial economist, and he was interested in the liquidity preference of savers because that was an important part of Keynes’ General Theory. The liquidity preference is the preference of consumers towards liquid assets, like cash or short term Treasury Bills, and Tobin showed how risk preferences were related to this important preference. He never would have guessed that his result would be a perennial reference in academic finance, but irrelevant in macroeconomics.
The idea is the cleverest, conceptually, in the development of the Standard Model. Start with the fact that investors are seeking to maximize return and minimize variance, so-called mean-variance preferences:
![]()
Where E[x] is the expected value, or mean, of x, and Var[x] is the variance, or volatility squared, of x.
Mathematically, this creates a set of indifference curves, where each point on the curve represent different trade-offs of volatility and return you are equally happy, or indifferent to. They curve because we usually list the x-axis in volatility, whereas the preference is for the square of volatility, variance. In figure 1.6 below, every point on the curved lines represents all the pairs of return and utility for which you are indifferent, they equal the same total utility, and each dominates any point on the lines below it, which represent a lower level of utility.
Figure 1.6
Utility Curves in Expect Return/Volatility Space

Now take a point on the y-axis, representing the risk free rate Rf. If you extend a line from this point, the line with the highest slope originating from Rf touches the highest utility curve. A consumer wants access to the highest sloping line from the risk free rate, in this picture, the maroon line touches the red curve, higher is better.
Figure 1.7
Reaching a Higher Utility Curve with Access to a Higher E(Rp)/Vol(p) Portfolio

A higher Expected Return/Standard Deviation asset, such as Rp High in figure 1.7 above, allows one to reach a higher level of utility, because it creates a line, and thus a feasible set, that touches the highest utility curve. This is the same as maximizing the Sharpe ratio, which is simply the expected return minus the risk free rate divided by the portfolio volatility, so what this means is, find the highest Sharpe for a portfolio of only risky assets. All the infinite combinations of volatility and expected return on a line connecting Rf , the risk free asset’s volatility and return, and Rp, the maximal Sharpe portfolio’s volatility and return, are feasible given varying combinations of the two assets, Rp and Rf. The highest Sharpe ratio portfolio allows one to reach the highest level of utility, regardless of the shape of your utility curve (that is, your particular risk tolerance).
Thus a complicated problem is reduced in complexity considerably, to simply finding the highest return/volatility portfolio. Given the statistics of returns as shown in figure 1.8, a parabolic hull of feasible portfolios is generated by combining the risky assets in every conceivable way, so we need to merely connect a line from Rf, to a point on that hull that generates the highest slope. This occurs at a point on the efficient frontier, a unique tangency portfolio that touches a line originating from the risk free rate.
Figure 1.8
The Efficient Frontier

Looking at figure 1.8 above, we see that the line from the risk free rate to the tangency portfolio. The tangency portfolio with the greatest ratio of Expected Return to Standard Deviation, is the optimal portfolio used in combination with the risk free asset to maximize one’s utility.
As this is the least obvious step in the creation of portfolio theory, let us prove this result. Suppose we construct a composite portfolio c that combines a Portfolio with Risky Assets, and a ‘risk-free’, return Rf. Let z represent the proportion invested in Portfolio of Risky Assets.
Then mathematically,
![]()
The expected return is simply proportional to the relative weighting on the risky portfolio
![]()
This is easy, expected values are linear operators, so one can avoid correlations in determining an expected value. Now, because the risk free asset has zero correlation and zero volatility, it can be ignored in the portfolio volatility estimation, and the volatility of the composite portfolio is even simpler, it is merely a function of the volatility of the Portfolio of Risk Assets.
![]()
That is, the volatility of the composite portfolio is merely a weighting of one’s investment in the risky portfolio. Solving for z, we get
![]()
Plugging back into equation at the beginning, we get

Or

This is the line generated from the
risk-free asset, Rf, through the portfolio of risky asssets, p. The
slope of which is maximized when  is
maximized, which is the slope of the line from the risk free rate to the risky
portfolio.
is
maximized, which is the slope of the line from the risk free rate to the risky
portfolio.
The point is, whatever your risk preferences (i.e., ‘a’ in mean-variance space), you are always using the same optimal tangency portfolio in combination with the risk free asset to reach your highest level of utility! The only difference is the proportion of these two portfolios. Your problem separates into two parts, independent of each other: find the tangency portfolio (same for everyone, to generate the highest sloping line from Rf), and then choose your particular combinations of Rf and the tangency portfolio depending on your risk preferences (different for everyone).
For example, consider your utility curves are represented in figure 1.9 below. Investor A, a conservative investor, invests about half his wealth in the riskless asset and half in the tangency portfolio, while investor B, an aggressive investor, invests all his wealth in the tangency portfolio, then borrows at the riskless rate rf and invests even more in the tangency portfolio. Risk lovers borrow to invest in the same portfolio that risk averse investors merely hold in modest quantities.
Figure 1.9
Risk Preferences are Irrelevant When Choosing the Optimal Risky Portfolio

The bottom line is that a unique risky portfolio, regardless of one’s risk preferences, is the optimal portfolio of risk assets, the tangency portfolio, and an investor’s relevant preference for risk would merely affect how much the investor put into this tangency portfolio.
The Capital Asset Pricing Model; CAPM
With 1000 assets, you needed to calculate 550,000 different covariances to generate an efficient frontier of portfolios so that one can find the optimal tangency portfolio. In the days before computers were common, this could simply not be done. But given Tobin’s Separation Theorem, the problem for an investor turns out to be trivial. In one of those moments of simultaneous discovery that suggests the result was truly inevitable, Lintner, Sharpe, Treynor, and Mossin, each independently discovered that you could merely look at an asset’s correlation with the aggregate market, not each individual asset. Given Tobin’s Separation Theorem, this is really kind of obvious.
Wealthier, and risk averse investors might allocate various amounts to this portfolio of risky assets, but within that risky portfolio, the weightings, or composition, would be exactly the same for all investors. Since equities exist in positive supply, in equilibrium, people have to hold them, and if any one holds them, everyone holds them, in the same proportion. Thus, prices must adjust such that everyone holds every asset is exact proportion to its supply in the market. Otherwise, people would demand more of a stock than exists, or not enough. The argument is an ‘equilibrium result’, because in equilibrium, supply has to equal demand, and so given everyone holds the same proportion of risky assets, their demand must proportionately match supply, or supply does not equal demand. Thus, the market portfolio must equal the demanded, optimal portfolio. QED. The market portfolio is the efficient risky portfolio alluded to by Tobin, and Roll (1977) points out that this specific hypothesis is really the essence of the CAPM.
The equation that generates the line connecting the risk free rate, to this optimal risky portfolio, ‘the market’, is called the Capital Market Line,
Figure 1.10
How Individual Stocks Relate to the Efficient Frontier

The figure 1.10 shows that there are two ways to receive an expected return of IBM: buy shares in IBM, or buy composite portfolio A, which appears to hold about half the market, and half the risk-free rate in this example. For a risk averse investor (as we all are) portfolio A is preferred to an investment solely in IBM since it produces the same return with less volatility (which in the 1960’s, was identical to ‘risk’). It is impossible to earn an expected return of IBM incurring less risk than that of portfolio A. The total risk of IBM can therefore be decomposed into systematic volatility, the minimum volatility required to earn that expected return and diversifiable volatility, that portion of the volatility that can be eliminated, without sacrificing any expected return, simply by diversifying. Investors are rewarded for bearing only the systematic volatility, but they are not rewarded for bearing diversifiable volatility, because it can be eliminated at no cost. Thus, a rational investor would never own a portfolio consisting of one stock, because its diversifiable risk is so large, and one would have to think that the expected return on that single stock is sufficiently high to offset this needless risk, a very high level of confidence and skill.
The basic proof goes something like this. Everyone is optimizing their portfolio’s utility, meaning they have solved the maximization problem for E(x)-a×var(x). This implies that for every asset within the portfolio, the following equation holds:
![]()
Every asset has the same marginal value. This is from the fact that for a large diversified portfolio, only covariance matter. Regardless of the individual’s risk preference (ie, ‘a’), this equation holds for all assets for any particular investor, even the risk-free asset:
![]()
Now, the risk free asset’s expected return is k, because sfm=0, implying
![]()
This is helpful because previously k was some unidentified parameter, whereas now it is some observable. The next trick, is to apply the equation to ‘the market’, that is, the covariance of the market with itself. This generates:
![]()
Rearranging, we have
![]()
Now, we have the unobserved parameter a as a function of observables. Plugging in for k and a, we now have
![]()
Rearranging, we get
![]()
The ratio of the covariance over the variance we call beta, because this is the coefficient in an OLS regression of a stock on the market portfolio. So we have
![]()
This is the Security Market Line, or the Capital Asset Pricing Model (CAPM), the essence of Sharpe’s Nobel Prize.
Figure 1.11
The CAPM

We can measure the amount of risk
now via beta. What is the price of risk? What is ![]() ?
The law of one price says that everything that costs the same has the same
return, or vice versa. In this case, an asset’s ‘cost’ is a linear function of
its beta, because the beta is sufficient to tell us its marginal addition to
the risk of our optimal risk portfolio, the market. Think of risk as a
commodity, something that people must hold in equilibrium. It costs the same,
per unit of risk, regardless of how it is distributed in the market, via a
single stock or a portfolio. The same beta must achieve the same return for
this cost via a single asset, or the market as a whole, because otherwise one
would buy the cheap one, sell the expensive one, and arbitrage the difference.
?
The law of one price says that everything that costs the same has the same
return, or vice versa. In this case, an asset’s ‘cost’ is a linear function of
its beta, because the beta is sufficient to tell us its marginal addition to
the risk of our optimal risk portfolio, the market. Think of risk as a
commodity, something that people must hold in equilibrium. It costs the same,
per unit of risk, regardless of how it is distributed in the market, via a
single stock or a portfolio. The same beta must achieve the same return for
this cost via a single asset, or the market as a whole, because otherwise one
would buy the cheap one, sell the expensive one, and arbitrage the difference.
A simpler way to prove the CAPM would be using arbitrage, an argument highlight by Richard Roll (1977). If the market is an efficient portfolio via Tobin’s argument, then the CAPM holds trivially. Say risk is solely covariance with the market, normalized by the variance of the market, then to achieve a beta of x using the market portfolio, invest x units in the market, and (1-x) units in the risk free asset. If x is 2, then you are leveraging yourself in the market (borrowing, 1-2 =-1, negative means borrow). If x =0.5 you are investing half in the risk free asset. More generally, given arbitrage, if you have an asset with a beta of x, it should have the same return constructed by leveraging the market to achieve a beta of x. So the expected return of the individual asset is on the left hand side of equation (1.22) below, the levered up portfolio that equals the same beta is on the right hand side. They should have the same return, because otherwise, everyone would invest in one at the expense of the other, which is not an equilibrium
![]()
Return on asset with βi is like being long βi units in the market with (1- βi) units in the risk free asset. Rearranging and substituting βi for x, we have
![]()
This is an arbitrage argument, and also an equilibrium argument. Indeed, one finds these arguments are generally identical.
The Security Market Line is the
CAPM, it is equation (1.23). Linearity in pricing implies no arbitrage, and
vice versa. It’s as if milk costs $2 a gallon, and then every fraction or
multiple of a gallon is merely $2 times how many gallons you bought. An
exposure to market risk, as reflected by beta, will give you the same return,
regardless of how it’s assembled: by individual stock, portfolio, risk, such
as represented by beta in the CAPM, generates a linear return, in the case of
CAPM, ![]() . This generalizes, or is
applicable, in every other theory in asset pricing.
. This generalizes, or is
applicable, in every other theory in asset pricing.
The keys are: risk aversion over aggregate wealth, risk measured as the covariance of the asset with the market (not the individual variance), and a linear price for risk (twice the risk generates twice the return above the risk-free rate). The covariance of the asset with the market is the key measure of how much risk, whereas the price of risk is reflected by the ratio of the risk premium, Rm-Rf, over the variance of the market, Var(Rm). In the CAPM, we simplify this to a beta, which is the covariance of an asset with the market divided by the variance of the market, times the risk premium. You can think of beta as the ‘how much’ and the equity risk premium as the ‘price’.
The Arbitrage Pricing Theory (APT)
The CAPM is a straightforward theory. You can test it. It predicts that all that is needed to estimate expected returns is the beta, where the beta is simply the ratio of the covariance of an asset is with the stock market’s return, divided by the variance of the market. The coefficients in a linear regression are often called ‘betas’ in introductory econometrics, ergo the name, beta (like when a child names his cat “kitty”).
But the CAPM was hardly definitive, even before one could see its empirical flaws. The basic two extensions are the Arbitrage Pricing Theory of Stephen Ross (1976), and the general equilibrium approach, which turn out to have very similar empirical implications. Unlike the CAPM, these are frameworks, not theories. There are no crucial tests of either of these approaches. The APT and general equilibrium approaches rationalize throwing the kitchen sink against an asset’s return, because risk factors are only constrained by your ability to articulate an intuition for risk, which considering the cleverness of top professors, is really no constraint at all. Even Fama 1991 called these theories a “fishing license” for factors (Fama 1991).
The APT is a simple extension of the logic applied in the CAPM, only to more than one factor using the ‘law of one price’, or arbitrage. The idea was simple. Assume a risk factor has a price like a beer costing $1 per can. Then a six-pack must cost $6, otherwise, one could arbitrage this buy either buying six-packs and breaking them apart, or buying individual beers and aggregating them into six packs. This holds for every factor relevant to an asset.
Assume a stock has several risk factors, things that are priced like in the CAPM, have risk like the CAPM (nondiversifiable), and measured like the CAPM (betas). For example, a three factor model would have the following form
![]()
A four or five factor model would
generalize in the logical way, with merely more terms. Thus each factor is
just like a little CAPM term, where the factor, ![]() has
a premium, an expected return over the risk free rate, just like ‘the market’
in the CAPM. Each firm has its own beta, β1, with respect to
each factor. In practice these are determined by regressing returns against
these factors, so in a multifactor model the problem is more complicated than
the simple ratio of the variance to the covariance, but if we accept the betas
come out of regressions, and regression packages come within Microsoft Excel,
it’s simple enough. The fundamental result relies on the same logic in the
CAPM. No matter how you achieve the amount of risk as represented by a beta,
it should cost the same regardless due to arbitrage, ergo, Arbitrage pricing.
If exposure to a risk factor generated a different return, via individual
stocks or portfolios, one would buy the cheap one, sell the expensive one, and
make risk free profits. If you measure the betas correctly, it should have the
same price no matter how it was constructed. Risk is all that matters, and so
it is priced consistently.
has
a premium, an expected return over the risk free rate, just like ‘the market’
in the CAPM. Each firm has its own beta, β1, with respect to
each factor. In practice these are determined by regressing returns against
these factors, so in a multifactor model the problem is more complicated than
the simple ratio of the variance to the covariance, but if we accept the betas
come out of regressions, and regression packages come within Microsoft Excel,
it’s simple enough. The fundamental result relies on the same logic in the
CAPM. No matter how you achieve the amount of risk as represented by a beta,
it should cost the same regardless due to arbitrage, ergo, Arbitrage pricing.
If exposure to a risk factor generated a different return, via individual
stocks or portfolios, one would buy the cheap one, sell the expensive one, and
make risk free profits. If you measure the betas correctly, it should have the
same price no matter how it was constructed. Risk is all that matters, and so
it is priced consistently.
Betas measure how much risk, and are a function of covariances, not volatility, though as a practical matter, equities with higher betas have higher volatility and vice versa. Risk premiums, well, where they come from is not essential to the APT, all we know is that if there is no arbitrage, whatever those priced risks are, return is linearly related the factors via their betas.
The APT assumes some unspecified set of risk factors, but since inception most researchers assume the first factor is the standard CAPM market factor, plus others are intuitive things that reflect risk: a measure of currency volatility, oil prices, inflation changes, industry risk, equity, country or regional indices, to name a few. Just write down these things like you would a return on the market portfolio, and regress them against a security to get the betas. These are all things that, like the stock market, changes cause us pleasure and pain, affecting our utility. Stocks that go up when we are surprised by good news are less valuable, riskier, than things that go up only a little when good new arises.
An early example of the APT was Barr Rosenberg’s Barra company that estimates factors for things like value, size, and industries, countries, volatility, price momentum, and various combinations (small cap-growth) therein, eventually coming up with over 50 such factors. The idea is that a long/short portfolio based on size (long the small stocks, short the big stocks), proxies some risk, and so these proxy portfolios are risk factors, because they reflect the relative return on a strategy focusing on value, size, or what have you. They have been offering there services since the 1970’s.
Actually, one need not even specify the factor as something intuitive. Factor analysis allows one to boil down a stock market’s volatility into statistical factors that often have no intuition at all. There are statistical techniques that generate time series of data that look like market returns, but they are really returns on portfolios that ‘explain’ the variance of the constituents. There will be a factor, or set of factors (i.e. returns), that explains most of the variance within the S&P500 one observes over time. In practice, this first factor is highly correlated with the equal weighted return on the portfolio. So the first factor in these approaches is somewhat of an equal-weighted market proxy. The second factor was smaller by a factor of 10 in terms of the ability to explain returns—a big drop off—and is not intuitively obvious to anyone what this correlated with, and less so for subsequent factors.
This makes the APT more generalizable, but also less useful, because some may choose to include a risk factor for inflation, or oil, and some not. Who’s to say what risk factors are priced? In the APT it is purely an empirical question, which has turned out to be much more ambiguous than expected. That is, theoretically, the equation is
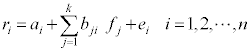
Interestingly, CAPM creator William Sharpe proposed a 12-factor model in 1992 for evaluating portfolio managers, suggesting the old guard has been moved to this approach, which is an extension of the CAPM.
The Stochastic Discount Factor (SDF)
The SDF approach is often called an ‘intertemporal general equilibrium model’. The financial work starts with the Merton (1971), expanded by Robert E. Lucas (1978), and Cox, Ingersoll and Ross (1985). It generates the basic implication that returns of assets are a function of some risk-free rate, plus a risk premium that is a function of the covariance of the return of that asset with the ‘marginal utility of wealth’. Things with high payoffs when the marginal utility of wealth is high have high payoffs when the level of wealth is low (because marginal utility declines with increases in wealth). The marginal utility of wealth can be proxied by a ‘state variable’ representing the state of something that affects utility, like GDP or consumption. As this state changes over time—due to recessions, changes in optimism about the future—this makes it is stochastic. As this affects the risk premium, it is thus a ‘stochastic discount factor’.
The real beginning of the SDF approach was when future Nobel Prize winners Kenneth Arrow and Gerard Debreu invented the concept of a state-space security, what would later be called Arrow-Debreu securities (Arrow and DeBreu, 1954). These theoretical constructs would pay off a unit if the state were achieved, zero otherwise, where the ‘state’ could be anything you could imagine: when stocks decline by 10% over the previous day and Fed Funds are above 5%. Such ‘state contingent’ thinking forms the basis of the Stochastic Discount Factor.
Discount Factors allow one to translate a dollar tomorrow into a dollar today. They are stochastic, in that they change over time, depending on how nervous or prosperous the aggregate economy is. For example, a higher interest rate would increase the discount rate, and discount factors should be higher when we are in good times, or there is little uncertainty about the future. Thus the discount factor should fluctuate over time, and this fluctuation will lead to varying returns even if payoffs are constant on average. In general, think of a discount factor as being less than 1, and
![]()
Where g is the ‘risk premium’ of say 4% and Rf the riskless interest rate of 5%. In absence of risk, the discount factor is merely the inverse of the gross risk-free interest rate, or 1/(1+Rf): higher the interest rate, the lower the discount rate, and vice versa. This would generate a discount factor like the following
![]()
The basic idea in asset pricing is that the price of a security is worth is discounted value of its payoffs, multiplied by the probability of those payoffs, as shown in the von Neumann-Morganstern Utility Function.
Because good times imply we have little need for stuff, and bad times not, this implies we should affect the discount factor for things that pay off in ‘good times’ versus ‘bad times’. It is higher in “poor” states because in those states of the world, the value of money is higher. Any asset paying off something in the future is merely the sum of the Discount Factors, times their payoffs, times their probabilities.
![]()
Here DF(S) is the discounted value of a dollar in state s tomorrow, where it is supposed to be different in the different states, because money is worth different amounts, depending on, say, whether there is a recession or expansion in that period.
Dividing through by P0, and one turns this from a relationship for prices, to one on gross returns (gross returns are simply net returns + 1, like a 5% is a net return, 1.05 is the gross return; P1/P0 is R), one gets
![]()
The sum of probabilities is just an
expectation, where![]() so we can write this
as
so we can write this
as
1=E[DF×R]
Which, for some unknown reason, DF was changed to M, and thus became
1=E[MR]
In the 1970’s economists began to prove mathematical properties that would be nice for the DFs to have. To get a flavor of this research, there was much rejoicing when it was proved theoretically the DFs had to be nonnegative, meaning, you would never get paid to potentially receive a dollar in some future state, as if this needed proving (Harrison and Kreps, 1980) The basic paradigm develops a momentum of its own via these theoretical discoveries and extensions. Rubinstein (1975) outlined the assumptions needed to reify a single consumer as a representative agent of the entire economy, and though these assumptions were insanely strong (for example, that everyone has the same beliefs about probabilities), once he outlined the assumptions, the use of a representative agent was defensible because Rubinstein proved this was appropriate under some basic assumptions, which were not really important because most economic assumptions, like perfect information and zero transaction costs, are not technically true (this inures one to absurdities).
Most importantly in this early period, they proved that arbitrage implies cash flows will be weighted the same regardless of security. This is really like the APT, which was introduced around the same time. Clearly, the idea was in the air, that if one security has a codicil that says you get $1 the S&P goes down 10% next year, that part of the security should cost the same no matter what security it is attached to, because its price is independent of the portfolio it may be in. Financial assets are always priced the same regardless of personal context due to arbitrage. More realistically, if a security should expect to do especially poorly in the next credit crunch, that aspect of the security adds or subtracts the same to every security that has this characteristic. Linearity in pricing of risk, just like the CAPM and APT. Another property of this approach is that risk is taken into account in terms of covariances. The only difference is this is the covariance with utility, not the market.
But where does the DF come from? Where do you get these discount factors for all these ‘states of nature’?
The answer is from the following idea. A dollar today can be transformed into X dollars tomorrow via an investment. The utility of a dollar today is the marginal utility of a dollar, based on how wealthy we are, etc. The utility of a dollar tomorrow is the marginal utility of a dollar then, based on how wealthy we are then. Let r represent the rate of return on the asset. The marginal value of a dollar today, equals the product of the marginal value of a dollar tomorrow, times the marginal value of a dollar tomorrow:
![]()
Here ![]() is
the marginal value of a dollar today, and
is
the marginal value of a dollar today, and ![]() the
marginal value of a dollar tomorrow. Today is represented by the subscript 0,
tomorrow 1, the ‘ superscript notes this is the derivative of utility, or
marginal utility, at that time.
the
marginal value of a dollar tomorrow. Today is represented by the subscript 0,
tomorrow 1, the ‘ superscript notes this is the derivative of utility, or
marginal utility, at that time.
If the interest rate is, say, 5%,
we can easily exchange $1 today for $1.05 dollars tomorrow via this interest
rate, a ‘transformation machine’. This can only be equilibrium if people’s
preferences value $1 today like they would $1.05 dollars tomorrow, otherwise,
they would either never save, or save everything and never consume, both of
which are counterfactual. We need the marginal value of a dollar today to
equal the marginal value of a dollar tomorrow, giving us equation (1.33)
above. Now, dividing by![]() , we get
, we get
![]()
Replacing ![]() with M we get
with M we get
1=E[MR]
Thus we are back to the DF formulation above, only now we have economic intuition for where the Discount Factor comes from, and in the literature call the discount factor M for historical reasons (MºDF). Though it has a more compelling origin that the APT, it works the same way, it values payouts in various states the same, regardless of the package.
Since M and R are potentially random variables, they must obey this following statistical law:
![]()
As the covariance was the key to the CAPM, using some very intuitive assumptions, there’s a neat proof in the appendix of this chapter showing how this approach leads to the CAPM as a special case, that is, back to .
![]()
This is the kind of result scientists love, that a preliminary model is a special case of a more general model that has weaker assumptions. The way the SDF approach based on utility functions and assumptions about growth processes, connects both to the APT which is merely founded on arbitrage, to finally the CAPM as a special case, is the kind of consistency that is very alluring to the mathematically minded. How could this be an accident? Only the truth could be so beautiful! As we shall see, never underestimate the ability of a mathematician to find a ‘beautiful explanation’ for any fact.
Factor pricing models follow this approach. They just specify that the discount factor is a linear function of a set of proxies,
![]()
where f are factors and a, b are parameters. (This is a different sense of the use of the word “factor” than “discount factor”). One can always work backwards from the desired set of factors that explain returns to a utility function M. The Arbitrage Pricing Theory (APT) uses returns on broad-based portfolios derived from a factor analysis of the return covariance matrix. The Intertemporal Capital Asset Pricing Model (ICAPM) suggests macroeconomic variables such as GNP and inflation and variables that forecast macroeconomic variables or asset returns as factors. Term structure models such as the Cox-Ingersoll-Ross model specify that the discount factor is a function of a few term structure variables, for example the short rate of interest and a few interest rate spreads.
So the Discount Factor approach suggests we look for things that are proxies of our marginal valuation of dollars tomorrow. Utility suggests that we look for things that proxy our wealth, because our aggregate wealth determines our marginal utility. Such things include the stock market, but also inflation, exchange rates, wage rates, consumption, oil prices, etc. Whatever you think affects people’s well-being could be a factor. A positive return on a security would be worth a lot more if you lost your entire savings that same year; the covariance of an asset with these hypotheticals determines its ‘risk’. The covariance of the payout matters, though instead of tying it to ‘the market’, as in the CAPM, we now tie it to the abstruse idea of your marginal utility tomorrow, or your valuation of money tomorrow.
So, just as in the APT, we are left with this unspecified multifactor model, though now we have motivation for the factors: things that are related to our marginal utility. The difference between the Discount Factor and APT approach is merely in the derivation. One is based purely on arbitrage, the idea that whatever risks exist are priced, they must be priced linearly according to their betas. The other, based on something more fundamental, the marginal utility of investors in various ‘states’, but the result is the same as the APT: we have risk factors (i.e., the price of risk) and their betas (i.e., the amount of risk).
General equilibrium models of asset pricing get down to Stochastic Discount Factors, which is really a different way to generate the same form as the APT, which is itself more general than the CAPM. Enthusiasts see this as the alpha and omega of finance, a unified field theory of derivatives, yield curves, equities, etc. The elegance and profundity of the SDF is essential in understanding the deep roots to the current paradigm in the face of its empirical failures.
Next Section (section 2) | Last Section (Intro) | Download pdf
Appendix: Proving the CAPM is a special Case of the Stochastic Discount Factor Model
Start with the basic equation of the Stochastic Discount Factor Model,
![]()
Can be rearranged to
![]()
Now, here’s where the algebra becomes interesting. Assume we are considering a risk free asset. It has no variance, so no covariance (ie, covariance with anything is zero). So this nails down E[M]:
![]()
The value of a dollar tomorrow is
negatively correlated with the expected market return given the concavity of
utility (higher wealth means we are richer, and thus value money less), the
value of a dollar tomorrow is therefore negatively correlated with the return
on the stock market. If the economy has a representative agent with a well
defined utility function, then the SDF is related to the marginal utility of
aggregate consumption. So replace ![]() with
with ![]() , so now
, so now
![]()
Now we already know that by
definition, ![]() , so replacing M with these
equations we get
, so replacing M with these
equations we get

Crossing out the U0’s we have
![]()
Apply this equation to the market
itself, so that ![]()
![]()
Then the marginal value of a dollar today is worth
![]()
Replacing ![]() with
with![]() ,
we have
,
we have
![]()
Which given the definition of β, is merely the CAPM equation
![]()
QED