


The Scope of the Empirical Failure
Risk Premiums Across Most Asset Classes are Usually Perverse
As the current extensions to the CAPM via Arbitrage Pricing Theory or Stochastic Discount Factors has no consensus on what that risk factors actually are, this creates a problem in criticizing the general proposition that some risk measure is not positively correlated with expected returns. The current theory is really a framework, as opposed to a theory, and so any single bit of evidence, such as the low return to highly volatile stocks, in isolation, merely suggest a flawed risk proxy. Yet fundamentally, the theory of risk premiums is based on the idea that we do not like things that covary with our wealth, broadly defined, because they increase our net wealth volatility. It seems reasonable to presume, therefore, that priced risk is somehow positively correlated with volatility, because volatility is positively correlated with CAPM betas, and any risk factor intuitively is correlated with the market as a whole.
Thus, the most damning evidence is the scope of the volatility-return failure across many asset classes. This evidence has never been presented as an argument for the failure of the conventional theory because as this theory cuts across several asset classes, each with their own measurement and stochastic characteristics, a neat statistical test is difficult if not impossible. But the welter of data is broad, and examples of a volatility-return relation are the anomalies, rather than the observation that risky securities have lower returns in a particular asset class.
A. Total Volatility and Cross-Sectional Returns
My 1994 dissertation was titled ‘Mutual Funds, Idiosyncratic Variance, and Asset Returns.’ It documented that idiosyncratic risk is negatively related to returns, and obviously has influenced my prejudices subsequently. I emphasized the ‘idiosyncratic’ because the idea that total volatility was inversely related to returns was considered absurd, regardless of the data, as this was prior to the behavioralist revolution so anomalies were viewed with much greater skepticism. Of course, the relation is the same whether one uses beta, total volatility, or idiosyncratic volatility.
Alas, this finding was sufficiently uninteresting to not merit a single fly-out, let alone an academic job offer, but I note why I am so interested in this subject, and clearly not using ex-post information to create a simple hypothesis. I was rather unmoved by the lack of reaction, because I felt I discovered an arbitrage, and hoped to implement my finding in the private sector. At my first job after graduate school I had an opportunity to present my arguments to an asset management business with several billions of dollars under management. As I was offering a product with a marginal (1-2%) return premium but lower volatility, this did not appeal to those in charge, highlighting that most investors operate not on Sharpe ratios, but rather, a deviation from the benchmark. Nonetheless, in 1996 I set up a C-corp with $120k of family money, and created the Falken Fund. It generated a 16.0% return from January 1997 through August 2002, a 12.1% return premium to the S&P500 over that period. This fund simply used the strategy of going long 30 stocks with below average volatility, but the highest 12 month prior return (taking into account momentum), rebalanced every 6 to 12 months.
I then finagled my way into a position at a hedge fund and abandoned my little experiment for a more substantial application. I applied long-short equity portfolios based on this insight within hedge funds from 2003 through 2006. After leaving a hedge fund in 2006 I attempted to start a new fund, I was then embroiled in 18 months of litigation where my old firm asserted that I could not volatility as a factor in returns in future activities, in spite of my prior use. My usage of volatility as an investment factor was potentially illegal, which severely curtailed institutional interest in my services. While this litigation was settled out of court in 2008, it highlights that I did employ this factor in actual portfolios in the aughts, and it was considered sufficiently valuable to underlay costly litigation (litigation, not imitation, is the sincerest form of flattery). The bottom line is that I identified the dominance of low volatility as a dominant return sector, and have applied it successfully with real money.
Ang, Hodrick, Xing and Zhang (2006) documented the relationship between idiosyncratic variance and returns, cross sectionally, and this was followed up by international corroboration (ie, non-US) showing the same thing. (Blitz and van Vliet, 2007, Ang, Hodrick, Xing, and Zhang, 2007, 2008). The key to presenting such a patently anomalous result is not presenting it as rejecting the general risk-return paradigm, but rather highlighting how nuanced the standard model is.
Figure 4.1 below shows the average excess returns for quintiles sorted by idiosyncratic volatility. Excess returns’, which are like the alpha in a market model that includes factors, in this case, the 4-factor Fama-French factors. You take the total returns, and subtract the ‘factor returns’, because the excess return is that which is ‘unexplained’ by the Fama-French factors. As these factors are generally positively correlated to variance, that merely increases the alpha, because total volatility and beta are positively correlated, meaning highly volatile stocks have a higher beta and higher expected return. But that’s all a distraction in this case, because the excess returns are ridiculously large: -15% annually for the highest volatility stocks. The following year, they documented this effect in 23 developed country markets and leave this finding as a global puzzle.
Figure 4.1
Annual Excess Returns to G-7 Equities Sorted by Idiosyncratic Volatility

From Ang, Hodrick, Xing and Zhang 2007, Table 7. Returns are annualized. 1963-03
B. Minimum Variance Portfolios
Researchers have investigated minimum variance funds since Haugen and Baker (1991), generally that a variance minimization algorithm applied to a large set of stocks, including a no-short-sales constraint, generates about a 30 percent reduction in volatility compared to common U.S. indexes without diminishing returns. If traditional measures of risk are unrelated to returns, this should be a straightforward way to create a portfolio with a Sharpe ratio that dominates the market. Curiously, all the papers that examined minimizing index volatility also found that not only can you create portfolios with much less variance than simple market indexes, but their returns were actually higher than the benchmarks (Schwartz 2000, Clarke, de Silva and Thorley (2006), Blitz and van Vliet (2007)). In each case, the higher return was unremarked, as if it had to be some sort of mistake, merely emphasizing the lower volatility feasible in a minimum variance focus.
I have constructed long-only, low volatility portfolios MVPs, for Minimum Variance Portfolios. New index weights are calculated for each on January 1 and July 1 based on the prior year’s daily returns, using a minimum variance minimization algorithm on the factors and factor loadings from Chris Jones’s heteroskedasticity-consistent version of Connor and Korajczyk’s principal components procedure.
Index weights are then constant for the next six months using a total return index, so there is no rebalancing bias due to equal-weighting daily returns of portfolio constituents. There is no survivorship bias because I use stocks that existed in the indexes at the beginning of the performance period, transaction costs are low as these are highly liquid stocks and I am only going long, and liquidity issues should be minor because we are only going long stocks within the major equity indexes. Thus, unlike the Fama-French size (SMB) portfolio, with its many illiquid stocks and shorted securities, the January returns for the MVPs are actually slightly less than their sample average, suggesting there are no significant institutional issues due to end-of-year tax strategies that show up in illiquid securities.
Minimum Variance Portfolios are prominent in advanced textbooks on portfolio theory, because they form the leftmost point in the convex hull representing the set of feasible returns in risk-return space. Theoretically, they include long and short positions in stocks. The long-only approach of an MVP is attractive because many obvious stocks we all wish to short (for example, Palm in the 3M spin-off of 1999) in practice cannot be shorted, or have a negative rebate. Rebate schedules and impossible-to-borrow lists are difficult to accurately recreate because these are over-the-counter markets. Furthermore, in many developed markets, one can short only 40 percent of the stocks, and proportionately more of the weak stocks everyone wishes to short. This makes long-short historical simulations difficult to interpret, because one can never be certain it was feasible to implement the short side of a portfolio-minimizing algorithm.
Jagannathan and Ma (2003) show that in constructing a global minimum variance portfolio, a no-short-sales constraint actually helps out-of-sample performance because in an unconstrained approach, recommended shorts usually have very high covariances with other stocks. Stocks that have extremely high covariances with other stocks tend to receive negative portfolio weights, and the no-short-sales constraint is equivalent to capping the sample covariances at reasonable level (alternatively, one can think of it as applying a Bayesian base rate to a covariance estimate that mitigates extreme correlations in sample). Hence, to the extent that high estimated covariances are more likely to be caused by upward-biased estimation error, imposing the nonnegativity constraint on position weights reduces the sampling error, and so a no-short-sales restriction is in practice a modest constraint in constructing a minimum variance portfolio, and makes the result something eminently feasible.
Looking at the past 10 years of data for the S&P500, eight years of data for the Nikkei and FTSE, and seven years for the MSCI-Euro Index, Table 4.2 shows that annualized volatility can be reduced by 30 to 45 percent within these indexes by simply reweighting the constituents in a way that minimizes the historical volatility, but is then applied to the out-of-sample returns. Furthermore, in each case, the numerator of the Sharpe ratio was also significantly higher. The FTSE, Nikkei, S&P500, and MSCI-Euro index would need annualized return increases of several percentage points to equalize the Sharpe ratios of their relevant MVPs. For example, the S&P500 has an annualized geometric return of almost zero, -0.58 percent, over the past 10 years, whereas the minimum variance subset portfolio generated a 6.58 percent annualized return over that same period. As the volatility of the S&P is about 21 percent versus 17 percent for the MVP, in a Sharpe ratio perspective, the S&P return would have to be about 10 percent higher, annually, to be comparable to the minimum variance portfolio for your mean-variance maximizing investor. Betas of the MVPs range from 0.52 to 0.67. Thus, as index funds dominate actively managed funds primarily because of their 1 percent cost advantage, the relevant advantage here is several orders of magnitudes higher in this sample periodd.
Table 4.2
Summary Statistics of Minimum Variance Portfolios versus Their Indexes
1998-2010
FTSE FTSE-M MSCI-Eur MSCI-M Nikkei Nikkei-M SP500 SP500-M
Avg Ann Ret 3.1% 6.9% 2.2% 2.8% 0.3% 0.8% 4.1% 8.2%
Ann StDev 15.3% 12.2% 19.8% 13.4% 19.9% 13.3% 16.7% 12.5%
Avg Geo Ret 0.7% 5.5% -1.7% 1.0% -3.7% -0.9% 1.3% 6.6%
Beta 0.66 0.59 0.49 0.46
Sharpe -0.22 0.11 -0.22 -0.12 -0.20 -0.09 -0.13 0.25
Libor 4.08% 2.59% 0.32% 3.48%
SP500-M, Nikkei-M, MSCI-M, and FTSE-M are the Minimum Variance Portfolios of the S&P500, Nikkei 225, MSCI-Euro, and FTSE 100 indexes. Each index is formed at the end of June and December using a long-only subset of the corresponding index, where portfolio weights minimize the portfolio volatility over the prior year’s daily returns. Beta is from regressing the daily returns of the MVP on its respective index. The Nikkei and Nikkei-MVP, FTSE, and FTSE-MVP use daily data from January 1 2001 to July 31, 2010, while the SP500-MVP and S&P500 use daily data from January 1, 1998, to July 31, 2010, and the MSCI-related indexes are from January 2, 2002, to July 31, 2010. The Sharpe ratio subtracts the average LIBOR rate for each currency from the annual return, divided by the annualized volatility of returns.
The returns in these samples are for geometric returns, and about 2 percent lower than the returns generated from an arithmetic averaging of the monthly returns. This is appropriate, I would argue, because this kind of strategy is a long-run strategy, not a market timing one, and so, the idea is over a long period of time, say 10 years, what were the returns. But the results are qualitatively similar using arithmetic returns.
If the most widely used equity indexes can be significantly dominated by simply applying the idea that risk is not rewarded using its very constituents, this suggests the failure of the CAPM and its extensions is not a mere academic finding, but something tangible to regular investors. For those demanding concrete proof that their standard approach works, in general, they should explain the Minimum Volatility Portfolio anomalies, because forming a portfolio based on the most conspicuous, and earliest, metrics of risk, is not data mining the way book-market or momentum might be—these are stock characteristics that should sit at the top of one’s list of things to measure against returns. The returns to these seemingly low risk portfolios are above the indexes, and for those who are skeptical of alpha and appreciative of relatively small edges, this move should be most attractive to index investors. Several fund complexes like Robeco and Unigestion have recently created funds explicitly targeting low volatility equities, and the only reason for them to not grow, would be if investors truly cannot trade their envy for greed. That is, those who can appreciate index funds relative to active mutual funds, should be able to appreciate MVPs.
C. Beta and Returns
Table 4.3 shows the returns to various portfolios grouped by their betas. This used the investable universe, which was assumed to have a lower bound at the twentieth percentile of the NYSE listed firms. As Nasdaq and AMEX firms are generally smaller, this gets rid of about half of the stocks actually listed, but it is more realistic in that it corresponds currently to about a $500MM market capitalization cut-off. Most institutional investors are wary of going much below this because it gets difficult to put on large positions, and using the percentile we can account for the upward drift in the average market capitalization of this period. No ETFs, REITs, closed-end funds, etc. All common stocks. Next, I simply calculated the beta of each stock against the S&P500 Index, using the past year’s daily returns, and ranked the stocks from low to high.
Table 4.3
Total Returns to Portfolios Sorted by Betas, 2/1962-7/2010
Beta-Low Beta-0.5 Beta-1.0 Beta-1.5 Beta-High S&P500
AnnRet 11.4% 11.7% 13.0% 12.6% 12.4% 10.6%
GeoRet 9.7% 10.4% 10.0% 5.7% 0.6% 8.3%
AnnStdev 13.1% 11.7% 17.4% 26.3% 34.3% 15.1%
Beta 0.58 0.57 1.04 1.44 1.81 1.0
Sharpe 0.25 0.33 0.20 -0.03 -0.17 0.12
Betas are constructed from monthly data, the prior 36-60 months as available. Beta-Low and Beta-High are the extremum 100 low and high beta stocks. Beta 0.5, 1.0, and 1.5 are from the 100 stocks nearest these numbers. Portfolios are formed every 6 months. Daily data is used for betas after 2000.
Data were taken from 1962 through July 2010. Only monthly data were used prior to 2000, but subsequent to that this was combined with daily return data, so that the beta estimates are better in the more recent period. Nonetheless, the older betas are instructive for purposes of analyzing the relation between beta and return.
Figure 4.5
Total Returns to Beta Strategies

We see that average annual returns are highest for the Beta 1.0 stocks. This portfolio contains only those stocks were the prospective beta forecast is closest to a beta of 1.0, thus trimming off the higher and lower beta equities. The beta 0.5, and beta 1.5, equivalently targeted those numbers. Over this period, we see the average beta actually experience by these portfolios was closer to one, reflecting some of the ineradicable mean reversion in beta. Nonetheless, they were relatively close to their beta targets. The high and low beta portfolios, meanwhile, were merely the 100 most extreme projected betas, and these betas varied considerably over the 47 year period.
Average returns are clearly not increasing in terms of beta, and so this suggests two interesting investing strategies.
First, a long only investor worried about beta risk could generate returns equivalent to the S&P500 bellwether index, but with significantly lower volatility and covariance with the business cycle, by emphasizing low beta stocks. Secondly, if one is concerned about benchmark risk, and avoiding lagging the market, one could target stocks with betas near 1.0, generating a portfolio with a beta near 1, but without the high flyers and really low beta stocks. This generates a 2-3% lift annually. Thus, given envy or greed as a motivator, the indexes are suboptimal aggregates.
D. Call Options.
Theoretically, beta—or any covariance with the elusive risk factor—measures the ‘how much’ of risk, and so if risk is priced, options with higher strike prices (ie, more out-of-the-money), have higher beta(s), which implies higher average return. Therefore far out-of-the-money call options should offer extremely high expected returns as a percent of their price. As underlying stocks always, in practice, have positive betas against ‘the market’, all calls will have positive betas that exceed the beta of the underlying stock, and call betas will increase in the strike price as the calls get further out-of-the-money. Hence, all calls will have positive expected returns and the expected returns will be larger for greater strike prices, because the betas, as a function of the call price, increase as you go out of the money.
For example, say you have a stock with a price of 100, and buy a call with a strike price of 120, expiring in 3 months. If the stock price rises to 110 over the next month, the call option will rise about 120%, while a long stock position rises only 10%. This is the implicit leverage in an option, that is, it is like being able to borrow 10 times one’s capital and invest in the market. It is exactly the same bet as an equity position, just higher powered. This is why greedy retail investors with inside information prefer options: you get the most bang for your buck in options if you know where stock prices are going.
Coval and Shumway (2001) prove that expected European call returns must be positive and increasing in the strike price provided only that (1) investor utility functions are increasing and concave and (2) stock returns are positively correlated with aggregate wealth.
Figure 4.6
Monthly Reruns for Call Options Ranked by their Sensitivity to Stock Price

Sophie Ni (2007). Table 5
Sophie Ni (2007) looked at data from 1996 through 2005, and found that the highest out-of-the-money calls, with one month to expiration, have average returns of −37%, over a month! Figure 4.6 above shows that if you bucket call options into groups based on their ‘deltas’, you find that call options, indeed, are indeed highly levered stock positions. Lower deltas mean the call option is less sensitive, in dollar terms, to a stock moving, but more sensitive, in percentage terms. Thus, an at-the-money call option with a delta of 0.5 move 0.5 dollars for every 1 dollar move in the underlying, while an out-of-the-money option may have a delta of 0.08. On a percentage basis, since the at the money option has a price of around 5, while the out-of-the-money option a price of 0.25, the percent change in price for the low delta option is much greater. The key to remember is that the average stock has a beta of 1.0, these betas range from 4 to 15—giving one 4 to 15 times the juice of the daily return. An option's beta is the beta of the stock, times the 'omega', which is a measure of the percent return in the option price given a 1% change in the stock price. If the omega on a Ford call option is calculated to be 1.6, then for every 1% change in the price of Ford the price of the call option will rise by 1.6%.
Not only is the average return negative for call options, these returns get worse the more implicitly levered, the more ‘risky’, the options become, in contrast to what is implied by the standard model (see Coval and Shumway 1999). Returns are negatively correlated with the betas. Investors basically are overpaying for lottery tickets when they buy options, and just like the lottery, the average payout is worse they more risk one takes. If there’s a risk premium in equities, it certainly is not amplified in options in any way, because you lose money, on average, buying leverage market positions via call options
E. Private Investments
Entrepreneurial investment, such as in small proprietorships (S-corps and private LLCs) is generally a highly undiversified investment for most entrepreneurs. The reasons are straightforward, in that when one person has a significant effect on the business through his effort and competence, it is natural that he should have the most ‘skin in the game’. This is a classic issue of moral hazard because a business manager, who has significant upside and, without ownership, no downside, is motivated to take wild risks on the theory of heads I win, tails the banker loses. However, if the manager is the majority owner, his failure should affect his net wealth too. About 75 percent of all private equity is owned by households for whom it constitutes at least half of their total net worth. Furthermore, households with entrepreneurial equity invest on average more than 70 percent of their private holdings in a single private company in which they have an active management interest. Despite this dramatic lack of diversification, private equity returns are on average no higher than the market return on all publicly traded equity. Figure 4.7 shows the basic results of Moskowitz and Vissing-Jorgensen (2002), that over an 8 year period, if anything returns to private business, be it partnerships, proprietorships, S corps, C corps, and two entirely different sets of data, there is no demonstrable premium Given an investor can invest in a diversified, and liquid equity portfolio, it is puzzling why households willingly invest substantial amounts in an asset with an equivalent return, but much higher volatility, including a positive correlation with the market.
Figure 4.7
Small Business Investments Returns
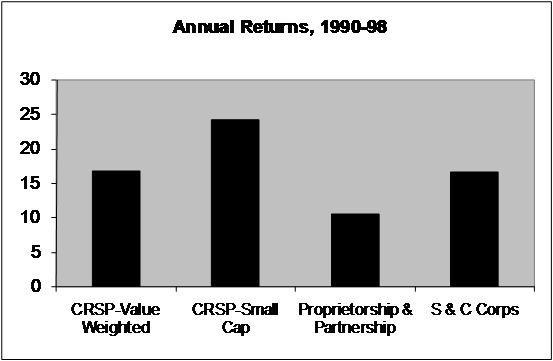
Table 4, Moskowitz, Tobias J, and Annette Vissing-Jorgensen. 2002. "The Returns to Entrepreneurial Investment: A Private Equity Premium Puzzle? "92(4), pp. 745-78
The forced nondiversification of a private equity investment, from a pure portfolio perspective, implies a requisite higher return. How much higher than the average public equity return would we expect the average private equity return to be? Using standard utility models to calibrate the hurdle rate that would make a household indifferent between investing in a portfolio of a single private firm, a public equity index, and T-bills, or a portfolio of just the public equity index and T-bills, researchers estimate that private equity risk generates a hurdle rate of about 10 percent higher the public equity return (Heaton and Lucas 2000). You should receive a huge premium for the large idiosyncratic risk you are taking, risk that unlike idiosyncratic risk in the market, is impossible to diversify away. Entreprenuers appear to be taking extra risk, for no extra return.
F. Leverage and Returns.
The Miller-Modigliani theorem states that regardless of the debt and equity proportions, the value of the firm is the same. As a firm increases its leverage using more debt, its equity concentrates the variable returns of the business on a smaller and smaller base, making them both riskier: the equity’s beta and volatility will increase, the debt will have a higher chance of defaulting. While total return is constant over a capital change, the equity and debt should both increase in expected return with an increase in leverage, as the lower debt return rises and becomes less of a weight in the total return calculation. The implication is that highly levered firms should have lower rated debt (junk), and more volatile equity, but because debt has a lower return than equity, the net, total return to all a company’s securities (debt and equity) is a constant.
Figure 4.8
Annual Return to Portfolios sorted by Market Leverage (Debt/Market Cap) Adjusted for Book/Market and Size Exposure
Penman, Richardson, and Tuna, 2007, Table 1
In figure 4.8 above, we see that leverage is, anomalously, clearly negatively correlated with returns. These researchers held constant size and book/market, so that this Market Leverage should not pick up these well-known anomalies. Higher leverage implies lower returns for equity even though this should increase risk of that equity, and thus should increase returns (Haugen and Baker 1996, Penman, Richardson, and Tuna 2007) . There have been no papers linking how leverage is positively related to expected returns, even though this result would have been consistent with a Nobel-prize winning theory. Empirically supporting Nobel-winning theory for the first time is worthy of a publication in a top journal, and for academics, this is their number one priority. The absence of a positive finding in this context is perhaps more powerful than the handful of negative results.
G. Mutual Funds
The original tests of the CAPM were on mutual fund returns, hoping to show that mutual fund performance would be explained by the new risk factor (Sharpe 1965, Treynor and Mazuy 1966). Subsequent work found no relationship between a stock’s return and its beta, and it was sufficiently uninteresting that in more recent work, the relation between beta and returns is addressed only as an aside in Malkiel (1995), who notes that a fund manager’s beta is uncorrelated with his fund’s average return.
As with leverage studies, the absence of any volatility or beta correlation with mutual fund returns is most relevant here, because it highlights an absence of confirmation in an area examined since the very beginnings of asset pricing theory. Absence of evidence is evidence of absence from a Bayesian perspective, not proof, but suggestive, especially when you know there has been a systematic, thoughtful search for such evidence. Carhart’s 1997 study of mutual funds is most well known for introducing ‘momentum’ as a factor, akin to Fama and French’s value and size factors, but it was also notable for the manifest irrelevance of ‘beta’ in his analysis. Good or bad, a mutual fund’s beta was never an issue in explaining the results, and so that paper hardly mentioned the null results, and instead centered on the importance of momentum as a ‘factor’ that explained the positive one-year persistence. Later studies of mutual funds by Russ Wermers (2000) do not even address beta.
H. Currencies
Uncovered Interest Rate Parity is a theory that connects current to future spot rates. This theory states that you have two ways of investing, which should be equal. First, you can invest in your home country at the riskless rate. So if the US interest rate is 5%, you can make a 5% return in one year, in USD. Alternatively, you can buy, say, Yen, invest at the yen interest rate (each currency has a different risk-free rate), and then convert back to USD when your riskless security matures. For this to be equal, you need something like
![]()
Where rusd is the US interest rate, etc. So, if you make 5% in USD, an American investor should receive that same return in yen, via the interest rate in yen, plus the expected appreciation/depreciation in the yen against the dollor. If the interest rate in yen is 1%, this means one expects the yen to appreciate by 4%. When the foreign interest rate is higher than the US interest rate, risk-neutral and rational US investors should expect the foreign currency to depreciate against the dollar by the difference between the two interest rates. This way, investors are indifferent between borrowing at home and lending abroad, or the converse. This is known as the uncovered interest rate parity condition, and it is violated in the data except in the case of very high inflation currencies. In practice higher foreign interest rates predict that foreign currencies appreciate against the dollar, making investing in higher interest rate countries win-win: you get appreciation on your currency, and higher riskless interest rates while in that currency.
Now the rates of expected return via the two investment paths can differ according to risk, of course. So one can imagine, looking at the yen, or the dollar, or various European currencies in the 1970’s, etc., trying to tie each to some measure of a home currency’s risk factor: consumption, the stock market.
Like high returns to low volatility stocks, it is difficult, but not theoretically impossible, to make sense of this. Robert Hodrick wrote a magisterial technical overview of the theory and evidence of currency markets in 1987. He summed up his findings in this paragraph:
"We have found a rich set of empirical results... We do not yet have a model of expected returns that fits the data. International finance is no worse off in this respect than more traditional areas of finance."
Hodrick looked at CAPM models, latent variable models, conditional variance models, models that use expenditures on durables, or nondurables and services, Kalman filters. None outperformed the spot rate as a predictor of future currency prices. Hodrick leaves off with the idea that ‘simple models may not work well’.
For the next 20 years, and many hedge funds specialized in the ‘carry trade’, which was as simple as it was successful: lend capital to high interest rate currencies, enjoy the high riskless rates and currency appreciation on the spot rate; borrow capital at the low interest rate currency, and make money on the depreciation of this debt over time. In 2008 these strategies suffered significantly, but the net effect is still there is no clear relation between risk and return in currencies.
Brunnermeier, Nagel and Pedersen (2008) noted that
Overall, we argue that our findings call for new theoretical macroeconomic models in which risk premia are affected by funding and liquidity constraints, not just shocks to productivity, output, or the utility function.
By ‘our findings’ they mean, the carry trade continued to work 30 years after being identified by Farber and Fama (1979), and it has continued as a puzzle because no reasonable risk factor can explain it.
I. World Country Returns
Erb, Harvey and Viskanta (1995) show similar returns between developed and nondeveloped countries, using data from 1979-1992. As the arithmetic returns are much higher than the geometric returns, he highlights those monthly returns for displaying a risk premium based on the volatility, but if you look at the geometric returns, they are about the same as the developed country data (13.5% for developing, 12.3% for developed. Using a more updated set of data from 1989 through 2000, Bansal and Dahlquist (2002) report approximately similar arithmetic returns (15.8% vs. 16.1%), but then using annualized geometric returns, the return for the developed countries was 13.8% vs. 6.7% for the developing countries.
Thus it is interesting that among country equity returns, there is no clear risk premium. Dimson, March, and Staunton (2005) find that the USA had about the same average return relative to short term debt from 1900-2005 compared to 17 other developed countries worldwide, about 5%. Figure 4.9 shows the volatility and returns for 17 countries over the 1900-2005 period.
Figure 4.9
Equity Premiums vs. Volatility for 17 Country Returns, 1900-2005

From Dimson, Marsh, and Staunton (2005).
It is strange that there is not a pattern among their returns in terms of volatility, because intuitively, those countries where the stock market index is especially volatile, would have a higher risk premium, as foreigners would not be able to invest sufficiently due to tax and institutional reasons, and eliminate the risk premium for this idiosyncratic risk. One can look for global risk factors that explain this, and the usual ones (eg, a world stock market index) do not work.
J. Corporate Bonds
The conventional corporate bond puzzle is that spreads are too high. The most conspicuous bond index captures US Baa and Aaa bond yields going back to 1919, which generates enough data to make it ‘the’ corporate spread measure, especially when looking at correlations with business cycles. Yet Baa bonds are still ‘investment grade’, and have only a 4.7% 10 year cumulative default rate after initial rating. As the recovery rate on defaulted bonds is around 50%, this annualizes to a mere 0.23% annualized loss rate. Since the spread between Baa and Aaa bonds has averaged around 1.2% since 1919, this generates an approximate 0.97% annualized excess return compared to the riskless Aaa yield, creating the puzzle that spreads are ‘too high’ for the risk incurred.
Altman and Bana (2004) and Kozhemiekin (2007) note there is no premium to ‘High Yield’ portfolios relative to investment grade portfolios, a set of bonds with a 3.84% average annual default rate from 1970-2005. Further, Altman and Stoneberg (2006) note that a bankrupt bond portfolio underperforms investment grade bonds. Both High Yield and Bankrupt bonds have more volatility and cyclicality than investment grade bonds, and do their worst when returns are most valued, in bad times. Junk bonds are intuitively, and academically, risky. Data from the Merrill Lynch High Yield index show an 8.47% annualized return relative to the 7.51% return of their investment grade index from 1987 through August 2010.
Table 4.3
Total Returns to Merrill Lynch Bond Indices, 1987-7/2010
High Yield Inv. Grade Treas Index
Ann Returns 8.47% 7.51% 6.83%
This might be seen as mild support for the idea that risk begets return, but it assumes one can buy the index using closing prices during this period, yet these indices are really an overstatement because how such indices have a systematic bias when portraying illiquid or unaudited asset classes. For a long time, average junk bonds bid-ask spreads were 5 points wide for bonds worth around 80, so it seems likely that transaction costs may detract a great deal from this difference.
Looking at the returns on Investment Grade and High Yield ETFs from December 2005 through August 2010.
Table 4.4
Total Return from June 1987 through August 2010
ETF Merrill Index
Inv. Grade 6.23% 6.44%
High Yield 5.65% 7.91%
This used 14 investment grade ETFs, and 46 high yield ETFs. Over this four and a half year period, the funds lagged the Merrill indices. Further, the lag was considerably gretar for the more volatile nad less liquid high yield fund as one would imagine.
Thus the closing prices of illiquid assets, such as in an index, will be a biased proxy for real returns if based on merely closing prices. If you take a couple percent off the high yield index due to price impact, commissions, bid-ask spread, junk bonds show no return premium to their intuitively less risky alternative, investment grade bonds.
The excess corporate risk premium puzzle pertains to one portion of the risk spectrum the difference between a 0.03% and a 0.3% annualized default rate, a distinction without a difference to most people. When one goes from a 0.3% to a 15% default rate, as one does when you go from BBB to C rated bonds, there is no return premium at all. Given reasonable expectations of transaction costs, and the actual difference between the high yield indices and actual high yield returns, it seem probable people extend into higher credit risk with a lower average return. It is difficult to see how the little risk is priced, the big one not, if risk is to have any consistent meaning. If the ‘corporate spread’ is a function of risk at one end, why is it not at the other, more intuitive end?
K. Yield Curve
he general shape of the yield curve is as follows. It rises until about 3 years, then flattens out. But this is deceiving because bonds have positive convexity, and so their returns are very non-normal at annual frequencies. Further, the higher maturity bonds have higher volatility, and this subtracts from their cumulative returns via the geometric averaging adjustment where we subtract the variance/2 from arithmetic returns. We should expect long bond holders to have long frequencies, and so this adjustment on monthly data is important.
Thus, I took data on US government bond yield since 1958 through July 2010, and constructed a set of annualized returns based on a buy-and-hold strategy. Each monthly return subtracted the Fed Funds rate, and included both the monthly price appreciation plus the coupon yield. These data are presented in figure 4.10 below.
Figure 4.10
US Treasury Data

As we can see, the returns to a funded position in bonds, an excess return, is very close to zero over this period. Indeed, buying 6-month T-bills funded at the Fed Funds rate was a money loser, and for the 1-year bond, about a zero return. But returns are increasing over maturity. Yet, the increase in yield from 5 years to 10 years is miniscule, around 20 basis points, and only 9 basis points from 10 to 20 years. The price volatility, meanwhile, increases consistently as maturity increase, and thus the Sharpe ratio peaks around 3 to 5 years, and declines a little as we move outward in duration. If risk provides the lift from 1 to 5 years, this risk is less important from 5 to 30 years.
One explanation is that many investors have a specific time horizon they are interested in, say 10 years. It is merely a difference in perspective, the nominal payout in 10 years is fixed as least risky if you are fixated on consumption in 10 years, as compared to a security that rolls over the short rate many times. But now the theory is at a stand-off. For someone who needs a fixed payment in 10 years, the 10-year fixed rate bond is risk free. Changes in yield cause it to have price variability, which is no concern to the person with a fixed payment in 10 years. On the other hand, some people buy assets, and don’t know when they will need it, or want its valuation to remain stable, as in the early naïve approaches to modeling bond risk. A risk-free asset in this context would be an asset such as a floating coupon that reset every month, and a fixed price. So the issue is, what is risky: a fixed payment in N years and a floating current price, or a fixed current price and a floating terminal payment as the yield curve changes? In this framework, risk is as justifiable as one’s favorite color, because everyone has different investing horizons.
The yield curve is usually used to demonstrate a risk-return premium by comparing two points on the yield curve, either the 1-year versus the 30-year, or the 1 month versus the 10-year. Price volatility, however, is clearly not the driver, because volatility continues to rise long after a return premium disappears, and no one thinks volatility as applied to stocks is related to risk any more.The key is, you span the 1- to 3-year fulcrum where the yield curve flattens out. Indeed, the six-month T-bill dominates the three-month T-bill in the sense that it generally gives one 20 basis points more return at small levels of interest rate risk; the shorter end of the curve is a free lunch for investors who prioritize the Sharpe ratio. The returns to bonds and bills are often noted as proof of a risk premium, usually by merely noting that one has higher return and higher volatility.
One clever answer is that we observe nominal bonds, and to the extent there is an inflation risk premium that increases as maturities increase, because if there is really high inflation, like in the 1970s, where the real returns on long-term bonds were negative, the more so the longer the maturity. Short-term T-bills were able to keep pace with inflation because one continually rolled them over. Therefore, if one has a demand for a fixed, real, future payment, then not a nominal fixed payment, but rather, the short-term rollover strategy is preferred. Thus, after three years, there is an exact canceling out between the inflation hedging properties of the shorter-term bond (which can be rolled over at higher rates in high inflation times), which preserves future value, and the low risk that comes from a fixed nominal payment of a longer maturity bond. A clever set of assumptions about the nature of inflation versus real interest rate risk could get this to work.
Yet looking at the inflation indexed Treasuries, TIPS, which started around and in data collected since 2004, show that the 5-to-20 year spread is virtually identical to the nominal Treasury spread over that period. The yield curve for TIPS out two years looks just like the regular U.S. bond yield curve, just shifted downward. When the yield spread between short- and long-term bonds was near zero nominally for U.S. bonds, it was near zero for the TIPS. It would appear that inflation risk premia are not relevant to shape of the yield curve.
L. Futures
Futures are derivative securities, bilateral agreements, one side to buy, the other to sell, at a future date, a spot commodity at a prespecified price. Futures returns are not driven by lower expected spot prices because such prices are reflected in a low current futures price (Black, (1976)). Unexpected deviations from the expected future spot price are by definition unpredictable, and should average out to zero over time for an investor in futures, unless the investor has an ability to correctly time the market.
What return can an investor in futures expect to earn if he does not benefit from expected spot price movements, and is unable to outsmart the market? The difference between the current futures price and the expected future spot price. Assume the current futures price is below the current spot price. Usually, this implies the expected spot price is above the futures price (we don’t truly observe the actual expected futures price, but this is generally true). On average, going long the futures makes money when it is below the current spot price because the futures price rises to the eventual spot price. At maturity, while the spot price may have fallen, the futures price has risen too. This is called ‘normal backwardization’ because if you put the futures prices out like a yield curve, the more distant futures prices are below the current price.
Figure 4.11
Forward Curves in August 2008. Gold in Contango, Copper in Normal Backwardization.

Figure 4.11 shows the term structure of futures for Gold and Copper in August 2008. Copper is in backwardization, while Gold is in ‘contango’, a fun name for the opposite. Historically, gold is always in contango, meaning, if you are long gold futures, you lose money on average as it rolls to maturity. Other commodities flop around, sometimes flat, sometimes in normal backwardization, and sometimes in contango. Harvey and Erb (2007) find that copper, heating oil, and live cattle were on average in backwardization, while corn, wheat, silver, gold and coffee were in contango, on average.
The expected roll returns (called because the futures prices ‘rolls’ to the current spot price over time), based on the current relation of the futures to the spot, are uncorrelated with the prominent risk factors (e.g., the market, value, and size factors, the Baa-Aaa yield spread). Changes in inflation adversely affects the roll returns from normal backwardization, while adversely affecting the roll returns for contango (see Gorton and Rouwenhorst 2005).
The question, obviously, is why are some futures in contango, and others in normal backwardization, from a risk perspective? A prominent early explanation put forth by none other than John Maynard Keynes, on why futures generate risk premium from being long, is that farmers grow wheat, say, and wish to hedge it by selling now, rather than waiting until the season is over. So a speculator buys the wheat now, and takes on the price risk, for which he must be compensated.
Futures allow operating companies to hedge their commodity price exposure, and since hedging is a form of insurance, hedgers must offer long-only commodity futures investors an insurance premium. Normal backwardation suggests that, in a world with risk-averse hedgers and investors, the excess return from a long commodity investment should be viewed as an insurance risk premium. It is easy to expand this to the other side, by focusing not on the producer of a commodity, but the purchaser. Say you are Boeing, and buy a lot of aluminum to build airplanes. If you hedge, you buy a futures today, locking in a price. Thus, whether you hedge by buying if you are a consumer, or selling if you are a producer, futures have an insurance-like characteristic. The key is knowing, between consumers and producers, who dominates the futures contracts. One explanation of the futures returns is that for some commodities, producers dominate the demand for insurance, and thus futures, in the other, consumers dominate.
In a diversified worldwide market, however, this reasoning does not work in explaining equilibrium returns. Asset pricing theory tells us that returns are a function of risk. And as most investors are not aluminum consumers, or corn suppliers, the net covariance with the risk factor should be at work. For example, the needs of a company, its preferences, are unrelated to its returns, which are a function of the change in the expectation of a company’s cash flows in relation to these other things we care about (for example, the S&P500). This is due to arbitrage, and because asset prices are set by supply and demand, where investors should be allocating capital in a way so that the price of risk, from any source, is the same whether it comes from futures or equities. If one can get the benefits of the futures roll and not be involved in the futures commodity—as most investors are not—this should be like idiosyncratic risk is, the CAPM: diversifiable, and so unpriced. And the expected roll returns (so-called because the futures prices rolls to the current spot price over time), based on the current relation of the futures to the spot, are uncorrelated with the prominent risk factors for equities (that is, the market, value, and size factors) or for corporate bonds (that is, the Baa-Aaa yield spread). Changes in inflation adversely affects the roll returns from normal backwardization, while adversely affecting the roll returns for contango.
There are predictable returns in futures returns, primarily from the movement in the futures price as the maturity date moves closer to the present, which is foreseen in the current relation of the futures price to the spot price. But what drives this, from a risk perspective, is a mystery.
M. Distress Risk
Early on in the size effect, researchers were at a loss to figure out what kind of risk that size, outside of beta, captured. The obvious risk, residual risk from these very small stocks, was diversifiable, and so not risk. Fama and French came upon the idea that both the value premium and the small stock premium were related to some sort of distress factor, that is, value stocks, whose price was beaten down by pessimists, and small stocks, which had less access to capital markets, probably had more risk of defaulting, or going bust, if the economy faltered. It may not show up in correlations or covariances, but that’s merely because such risks are very episodic, like the risk of a heart attack: The first symptom of a heart attack is a heart attack.
Ilya Dichev had documented this back in 1998, but this finding could be brushed off because he presumably had a poor default model (he used the Altman Model). But then several others documented a similar result, and finally Campbell, Hilscher, and Szilagyi (2006) find the distress factor can hardly explain the size and book or market factors; in fact, it merely creates another anomaly because the returns are significantly in the wrong direction. Distressed firms have much higher volatility, market betas, and loadings on value and small cap risk factors than stocks with a low risk of failure; furthermore, they have much worse performance in recessions. These patterns hold in all size quintiles but are particularly strong in smaller stocks. Distress was not a risk factor that generated a return premium, as suggested by theory, but rather a symptom of a high default rate, high bond and equity volatility, high bond and equity beta, and low equity return.
While I was at Moody’s in 2000, I was able to use their database of ratings back to 1975 and find that the rate of return lined up almost perfectly with the rating, with AAA having the highest return, C the lowest. Updating that data using S&P ratings, and used the rating in June, to form a portfolio over the following 12 months, a very straightforward strategy. I use 1987 as the starting point here because prior to this junk bonds, those with rating below investment grade, were small in number, as there was a structural shift in the junk market in the late 1980’s when these instruments started to have good pricing data (this does not change the results anyway).
Figure 4.12
Portfolios were formed every June. Firms delisting within the 12 months were then reallocated to the remainder of the portfolio

The returns are pretty flat until you get to the signature junk bonds, the Bs, and then it falls precipitously, and the Cs are even worse. Thus, the equity returns to firms with low financial strength are low, and their debt does not seem to compensate either. High risk, from a financial distress perspective, appears negatively related to returns for agency rated companies. When considered in conjunction with the flat to lower returns for B rated debt, this suggests a negative risk premium.
N. Movie Production
A paradox in the movies is that their rate of return is around 4 percent and the risk is higher than most industries. Art DeVany (2003) found that between 1986-99 G-rated movies generated lower volatility and approximately the same returns as R-rated movies, though there was a clear preference towards R-rated movies (over 1000 R-rated movies and only 60 G-rated ones). But movies has a strong pareto distribution, where the mean is much higher than the median or mode. It seems everyone is betting on the next Titanic, because the very highest grossing movies are R rated.
Figure 4.13
Movie Gross Return and Volatility by Rating
2015 movies from 1985-96

Devany and Walls (1999)
O. Sports Book
Bets on high probability–low payoff gambles have high expected value and low probability–high payoff gambles have low expected value. For example, a 1-10 horse having more than a 90% chance of winning has an expected value of about $1.03 (for every $1 bet), whereas a 100-1 horse has an expected value of about 14 cents per dollar invested (Hausch, D, Lo, and W Ziemba. 1994).
This bias has appeared across many years and across all sizes of race track betting pools. The effect of these biases are that for a given fixed amount of money bet, the expected return varies with the odds level. The favorite long-shot bias is monotone across odds and the drop in expected value is especially large for the lower probability horses. For bets on extreme favorites, there is an positive expected return. For all other bets, the expected return is negative. Ziemba, W. and D.B. Hausch (1984) document the favorite long-shot bias is monotone across odds and the drop in expected value is especially large for the lowest probability horses (worse than 50-1).
P. Lotteries
The annual per capita lottery expenditure in the US is about $170, and the rate of return is about -47%. It clearly presents a challenge to the idea that people are looking at these games on a risk-return continuum, and motivated the earliest inflected utility functions (Friedman and Savage (1947). These investments clearly cater to what is commonly called those seeking risk, or positive skew, in particular. There are two primary characteristics of lotteries. First, poor people play them more, in both relative and absolute terms, than wealthy people. Bhattacharyya and Garret (2006) find that those with household income of less than $25,000 spent $575 on lotteries on a per capita basis. This spending was substantially more than spending by those with a household income over $100,000 ($196). The people who can least afford it, buy the most of it.
Garrett and Sobel (2004) find the popularity (sales) of lotteries found that average payout (expected return), but the size of the top prize was highly significant. In other words, the $100 million super lotto has the most sales even though the probability of winning is so small it basically is outside the realm of intuition (1 in 150 million). People who bet seem to prefer those bets that offer the worst odds, but the greatest payout. Gambling seems to be totally outside the assumptions of risk aversion, and is the common motivator for Prospect Theory applications.
Q. Total Volatility and Aggregate Volatility and Returns
The most basic risk models assume that the expected return on an asset is proportional to the expected nondiversifiable variance of the asset: the higher the variance, the higher the expected return. Modern models tend to focus on some abstract thing we don’t like, like declines in consumption, wealth, or output, but those bad states are generally coincident with higher volatility, as volatility increases when the economy is doing poorly. And so what do we see? Some research documents a null relationship between volatility and future returns, some find a negative relationship (Campbell (1987), Whitelaw (1994), Nelson (1991).
Sharpe and Amromin (2005) used survey data, and found investor expectations were totally inconsistent with standard models. They found that when investors have a more favorable assessment of macroeconomic conditions, they tend to expect higher returns. Second, they found that the expectation of more favorable economic conditions has a strong negative effect on expected stock market volatility. This finding is totally incompatible with standard models. Sharpe and Amromin’s result really puts the standard model in a box. Unlike the CAPM betas, for which we can say we 'just don't know the true market portfolio', this result takes fewer assumptions, so its empirical failure is all the more fatal to the core financial theory. People should be increasing their expected returns in volatile markets, and on average that should manifest itself in actual returns. We don't see that in actual returns, or in surveys of expected returns.
An example of this finding is a Gallup poll put out by Paine Weber (Graham, Benjamin and Jason Zweig. 2003). In 1998, at the beginning of the stock market boom, they surveyed an expected return of 13% from investors. After back to back 20%+ returns, when the Nasdaq doubled, investors raised their expectations to 18% in February of 2000, right before the peak. Two years later, after a 50% correction, and a 50% rise in the VIX (a measure of expected volatilities), they anticipated only a 7% expected return. So from a Sharpe ratio perspective, when investors expect a high numerator, they expected a low denominator. They expect good times to be high returns and low risk, and bad times to be low returns and high volatility.
R. Initial Public Offerings
An initial public offering has a great deal of uncertainty, especially for an economist wishing to apply a factor sensitivity to it, because there is no time series. One usually applies a factor based on its characteristics, such as size, book/market, and perhaps industry. But without a track record, these assignments are highly uncertain in the Keynesian/Knightian/Ellsbergian sense. One would expect, given uncertainty aversion, for these stocks to have positive returns to compensate for this risk.
Examining IPOs from 1970-2007, Jay Ritter finds the geometric average return for these IPOs five years after issuance are 3.8% below size-matched firms (http://bear.warrington.ufl.edu/ritter/IPOs2008-5years.pdf). People who buy IPOs pay a premium, perhaps on the hope of buying the next Yahoo! or Google.
S. Analyst Disagreement
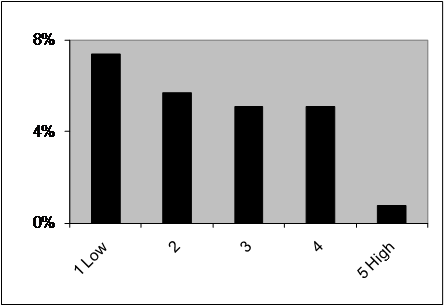
Differences of opinion should proxy for parameter uncertainty, a perhaps better estimate of risk (see Hansen and Sargent. 2001). Using analysts’ earnings forecasts as a proxy for differences of opinion among investors, Karl Diether et al (2002) find the quintile of stocks with the greatest opinion dispersions underperformed a portfolio of otherwise similar stocks.
Each month, they take stocks and sort them into five groups based on size (market cap), and then within these groups, sort again into quintile based on analyst forecast dispersion, as measured by the ratio of the standard deviation of analyst current fiscal year annual earnings per share forecasts to the absolute value of the mean forecast. They find that the stocks with the higher dispersion in analyst’s earnings forecasts earn significantly lower returns than otherwise similar stocks. Specifically, the highest dispersion group had a 9.5% annual return deficit over the 1980-2002 period.
Diether et al note higher estimate dispersion is positively related to Beta, volatility, earnings variability, yet, because the returns go the wrong way (lower return for higher volatility), they note “our results clearly reject the notion that dispersion in forecasts can be viewed as a proxy of risk”. Thus, in spite of being correlated with all things intuitively risky, like beta, volatility, and size, but uncorrelated with value or momentum, the correlation with returns proves it is not correlated with risk, because the one thing we know about risk, is that it is positively correlated with returns.
T. Trading Volume
Another metric of disagreement is the amount of trading volume in a stock, normalized by its stock volume. A stock may turnover 50% of its stock a day, suggesting 1) it is a useful factor proxy or 2) there is a lot of disagreement about its prospects. On average, if disagreement leads to more buys and sells, we should see a higher return to these stocks. Of course, we do not. In the US, since 1997, I created an index of stocks in the top 1500 that had the highest trading volume/shares outstanding, each six months. The annualized geometric return for these high volume stocks was 1.6%, vs 9.7% for the low volume stocks. The high volume stocks tend to be highly correlated with higher beta portfolio returns, and low volume with low beta stocks.
Figure 4.14
Total Return to various portfolios, 1998 through July 2010

Portfolios include 100 of those in the extremums for beta, or turnover, chosen each 6 months. Turnover is shares traded/shares outstanding
U. The Equity Risk Premium
One of the most important constants in finance is the equity risk premium, that expected return on the signature risk asset, equities, over the risk free alternative (usually, long-term Treasuries). It's the one risk premium that is generally considered positive, too large even, which is a relief because in most areas the returns are decidedly negative for taking more risk. Estimates in the early 1990s were about 8%, though most estimates today are around 3% annually (see Welch (2009)). Is the equity premium really zero? Consider the following annualized adjustments that mainstream economists apply piecemeal, though when considered in total take the current estimate well below zero:
Geometric vs. Arithmetic Averaging: 2%. This is where a stock going from 100, to 200, back to 100 has an arithmetic return of +25%, the geometric lower, at zero. Geometric is relevant to the long-term investor who is not rebalancing his investment each year. The adjustment is approximately the arithmetic return minus half the annualized variance divided by 2, so if the US equity volatility on average is 20%, the variance is 4%, divide by 2 is 2%. Dimson, Marsh, and Staunton (2006) actually look at specific country indices to arrive at this same number.
Survivorship Bias/Peso Problems: 3% The US is one of the best markets in the 20th century, so not a representative data point for an 'average' going forward. Czechoslovakia, Hungary, Poland, Russia, and China all experienced -100% returns, which are probably relevant datapoints for a forward looking US equity premium. The Peso problem literature points out that low probability events, such as something that happens 2% of the time annually, is often not observed in sample (see Rietz (1987). Barro (2005) surveys a number of developed on less developed financial collapses in the twentieth century and finds that this adjustment suggests a 3% reduction to equity risk premia.
Taxes: 3% Gannon and Blum (2006) calculate the after tax return to the S&P500 assuming 20% turnover from 1961-2005, using actual capital gains and dividend top-tier tax rates over this period. The average marginal tax rate—federal and state—for the top tier was 56% over this period, and the average capital gains tax 36%. This adjustment turns a 10.62% return into a 6.72% return, which is not much above the Long Term Municipal Bond Buyer Index return of 6.14%.
Adverse market Timing: 3%. Stock inflows, measured as new issuances of equity minus stock buybacks, are positively correlated to recent stock returns: people invest more new money into stocks after good times, not bad. This pattern hurts investors because of the nature of stock returns over time. An index may move from 100, to 200, to 100, and this return is zero if viewed at periodic returns, yet if one is investing equal share amounts each period—and thus correlated dollar amounts that are correlated with the returns—the return is actually negative. Dichev (2005) looked at a variety of indices, and equity net inflows, and finds this adjustment reduces returns by 1.3% for NYSE/AMEX for the period 1926-2002, 5.3% for Nasdaq from 1973-2002, and 1.5% for 19 major international stock exchanges from 1973-2004.
Transaction Costs: 2%. Transaction costs include commissions, fees, spreads, and price impact. While commissions and fees are straightforward, these are currently small relative to the spread and price impact. Indeed, liquidity providers profit from commissions, spread, and market impact, and so they often play ‘bait-and-switch’ in marketing, akin to how razor manufacturers sell their razors below cost and make it up on the razor blades.
Historically, commissions were about 60 cent/share until the 1975 deregulation, and are currently w about 2 cents a share (about 0.1%) on average. Plus, mutual funds often had 8.5% fees. Trade impact is rarely mentioned, but for an institution it is unavoidable, at least 0.2% one-way, and for retail investors with large positions, considerably higher.
Lastly, the bid-ask spread will cost you about 0.25% on average if you cross it, much more historically. An index fund may offer a near zero, even a negative transaction costs (they benefit from market power when lending out shares for short-sellers). Yet these are a small proportion of investors today, and for most of the twentieth century were not relevant. For the marginal investor, the sum of commission, bid-ask, and trade impact costs, is around 2% annually.
It is important to note that as a general rule, transaction costs increase the more volatile the market. The Plexus Group estimated that the more volatile Nasdaq equities cost about 50% more than AMEX or NYSE listed stocks (Plexus Group, 2001).
Kenneth French discussed trading costs in his 2008 American Finance Association Presidential Address, and estimated trading costs at around 0.11 percent in 2006 . At Deephaven I was involved with some high frequency equity strategies (investment horizons less than one month), and so we had to estimate the trading costs because on a long short portfolio. Using thousands of transactions, and comparing my fill price with the price at open when I traded against by fill price, I was able to estimate both the cost of crossing the spread and a price impact, and these varied by the amount we were trading, whether it was a long or short, whether we were initiating or closing a position, and so on. Our 0.2% cost was for a trader whose full time job involves minimizing this cost, using sophisticated algorithms refined via a large database that is impossible for your average retail investor to create, and direct market access software that retail investors do not have. Thus, I find French’s estimate preposterous. Most traders, especially retail traders, are not measuring, and so can not minimize this cost, and it is probably an order of magnitude higher for retail traders as brokers play bait and switch with commissions, trade impact, the bid-ask spread, funding costs, and other fees.
The bottom line is these are all individually very reasonable adjustments, each promoted in solid journal articles, claiming to ‘half’ the equity risk premium. Their net effect, however, is to demolish the equity risk premium. Like the evidence in the OJ Simpson murder trial, you can throw out any 1/2 of the evidence and the equity premium is no more than zero. A conservative estimate for each of these issues, added up, turns the average 5% equity risk premium into zero.
Table 4.5
Equity Premium Adjustments
Geometric vs. Arithmetic Averaging 2.0%
Survivorship Bias/Peso Problems 2.0%
Taxes 3.0%
Adverse Market Timing 3.0%
Transaction Costs 3.0%
Sum 13.0%
Surveys of hundreds of academic professors (Welch 2008, Fernandez 2010), suggest they assume a 5-6% equity risk premium. Welch notes the geometric-arithmetic adjustment explicitly, and this is estimated to be only 0.75%. Presumably, the survivorship bias and adverse market timing is implicit in these forecasts, and taxes and transaction costs are then ignored. I think these estimates are wrong.
Summary
In sum, the data on risk and returns does not seem consistent with any general risk premium story. Table 4.6 below assigns assets classes to various high level inferences of a risk-return pattern.
Table 4.6
Asset Classes and the Basic Risk-Return Nexus
|
Positive Risk Premium |
Zero Risk Premium |
Negative Risk Premium |
|
· Short End of Yield Curve · BBB-AAA Corporate Spread · Arithmetic Average of Nominal Equity Returns |
· Equity Country Returns · BBB to B Bond Return · Futures · Private Investments · Movies · Mutual Funds
|
· Equities o Betas o Volatility o Financial Distress o Trading Volume o Analyst Disagreement o Equity Options o Trading Volume o IPOs o Post Fee, post tax, survivorship free, internal rate of return on equities · Lotteries · Low Odds Sports Betting · Equities over Time · Currencies · Horse Racing |
If one‘s education was unaware of utility functions one would have to look at these data and say that volatility is inversely correlated with returns. The only clear area that a risk premium appears is in the BBB-AAA spread, the short end of the yield curve, and the equity risk premium excluding taxes, transaction costs, and market timing. They are exceptions to the rule. The theory that risk proxied by the intuitive concepts such as volatility, CAPM betas, or uncertainty is positively correlated with average returns fails when applied to volatility, movies, beta, developing country equities, aggregate volatility and aggregate returns, gambling, lotteries, options, financial leverage, financial distress, currencies, mutual funds, small businesses, analyst forecast dispersion, IPOs, and futures. These are not minor lacunae, but the heart of the risk-return theory, because it suggests any potential stochastic discount factor positively correlated with returns will be higher for firms that are intuitively safe. Even if conditional risk premia are time varying, risky characteristics are sufficiently autocorrelated to identify portfolios with greater volatility, downside tail risk, and covariance with the business cycle, and such assets with these characteristics do not have higher average returns. As a first approximation, volatility should be generally positively correlated with returns if the risk premium is to have any meaning in an asset pricing theory given its positive correlation with most time-varying risk proxies.
Last Section | Download PDF | Next Section